题目内容
12. 阅读下列材料:小华遇到这样一个问题:
阅读下列材料:小华遇到这样一个问题:已知:如图1,在△ABC中,三边的长分别为AB=$\sqrt{10}$,AC=$\sqrt{2}$,BC=2,求∠A的正切值.
小华是这样解决问题的:
如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.
(1)如图2,△DEF中与∠A相等的角为∠D,∠A的正切值为$\frac{1}{2}$.
(2)参考小华的方法请解决问题:若△LMN的三边分别为LM=2,MN=2$\sqrt{2}$,LN=2$\sqrt{5}$,求∠N的正切值.
分析 (1)先证明△DEF∽△ACB得∠D=∠A,根据tan∠A=tan∠D即可解决.
(2)构造一个△RKT∽△MLN得∠T=∠N,根据tan∠N=tan∠T即可解决.
解答 解:(1) 由图2 可知DE=2,EF=2$\sqrt{2}$,DF=2$\sqrt{5}$,AB=$\sqrt{10}$,AC=$\sqrt{2}$,BC=2,
由图2 可知DE=2,EF=2$\sqrt{2}$,DF=2$\sqrt{5}$,AB=$\sqrt{10}$,AC=$\sqrt{2}$,BC=2,
∵$\frac{DE}{AC}=\frac{EF}{BC}=\frac{DF}{AB}=\sqrt{2}$,
∴△DEF∽△ACB,
∴∠D=∠A,
∴tan∠A=tan∠D=$\frac{1}{2}$,
故答案分别为∠D,$\frac{1}{2}$
(2)在图3中,作一个△ RKT,使得PK=$\sqrt{5}$,RT=$\sqrt{10}$,KT=5,
RKT,使得PK=$\sqrt{5}$,RT=$\sqrt{10}$,KT=5,
∵LM=2,NM=2$\sqrt{2}$,LN=2$\sqrt{5}$,
∴$\frac{RK}{LM}=\frac{RT}{MN}=\frac{KT}{LN}$=$\frac{\sqrt{5}}{2}$,
∴△RKT∽△MLN,
∴∠T=∠N,
∴tan∠N=tan∠T=$\frac{1}{3}$.
点评 本题考查相似三角形的判定和性质、勾股定理、三角函数的定义等知识,学会用转化的数学思想解决问题,构造一个三角形和已知三角形相似是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
3. 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若
如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若
∠A′DC=90°,则∠A的度数为( )
 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若
如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A的度数为( )
| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
17.在-(-2)、-|-2|、-22、(-2)2这四个数中,最小的一个数是( )
| A. | -(-2) | B. | -|-2| | C. | -22 | D. | (-2)2 |
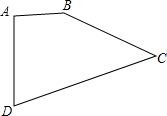 如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.
如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积. ABCD是圆内接四边形,过点C作DB的平行线交AB的延长线于E点,求证:BE•AD=BC•CD.
ABCD是圆内接四边形,过点C作DB的平行线交AB的延长线于E点,求证:BE•AD=BC•CD.