题目内容

4．先化简，再求值：$\frac{{x}^{2}-5x+6}{3{x}^{2}-3x}$÷（1-$\frac{3}{x+1}$）（1+$\frac{2}{x-3}$），其中x=$\sqrt{3}$．

分析 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．

解答 解：原式=$\frac{（x-2）（x-3）}{3x（x-1）}$÷$\frac{x-2}{x+1}$•$\frac{x-1}{x-3}$
=$\frac{（x-2）（x-3）}{3x（x-1）}$•$\frac{x+1}{x-2}$•$\frac{x-1}{x-3}$
=$\frac{x+1}{3x}$，
当x=$\sqrt{3}$时，原式=$\frac{\sqrt{3}+1}{3\sqrt{3}}$=$\frac{3+\sqrt{3}}{9}$．

点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案
相关题目
14．计算：$\sqrt{12}$+|-3|-2cos30°+（-1+$\sqrt{2}$）0．
15．已知点（-1，y1），（2，y2）都在直线y=$\frac{1}{2}$x+b上，则y1，y2大小关系是（　　）
A．y1＞y2B．y1=y2C．y1＜y2D．不能比较
12．阅读下列材料：小华遇到这样一个问题：
已知：如图1，在△ABC中，三边的长分别为AB=$\sqrt{10}$，AC=$\sqrt{2}$，BC=2，求∠A的正切值．
小华是这样解决问题的：
如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．
（1）如图2，△DEF中与∠A相等的角为∠D，∠A的正切值为$\frac{1}{2}$．
（2）参考小华的方法请解决问题：若△LMN的三边分别为LM=2，MN=2$\sqrt{2}$，LN=2$\sqrt{5}$，求∠N的正切值．
19．如图是由六个棱长为1的正方体组成的几何体，它的左视图是（　　）
A．B．C．D．
9．下列四个数中，负数是（　　）
A．|-2|B．-22C．-（-2）D．$\sqrt{（-2）^{2}}$
16．在-4，0，2.5，|-3|这四个数中，最大的数是（　　）
A．-4B．0C．2.5D．|-3|
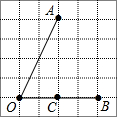13．在如图所示的方格图中，虚线叫格线，格线的交点叫格点，点C是∠AOB的边OB上的一点，解答下列问题：
（1）过点C和图中的另一个格点D画OA的平行线CD；
（2）过点C和图中的另一个格点E画OA的垂线CE，交OA于点F；
（3）线段CF的长度是点C到直线OA的距离，线段OF的长度是点O到直线CE的距离．因为直线外一点到直线上各点连接的所有线段中，垂线段最短，所以线段OC、CF的大小关系是CF＜OC．（用“＜”号连接）
14．某校七年级学生总人数为800，其男女生所占比例如图所示，则该校七年级男生人数为（　　）
A．500B．400C．384D．416

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网