题目内容
16.已知△ABC,分别以AB,AC为边在△ABC外侧作△ABD和△ACE,使AB=AD,AC=AE,且∠BAD=∠EAC,BE,CD交于点P.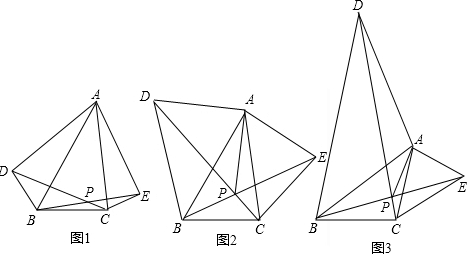
①如图1,求证:CD=BE;
②如图2,当∠BAD=60°时,求证:PD=PA+PB;
③如图3,当∠BAD=90°时,若∠BAC=45°,∠BAP=30°,试探究线段BD,CD之间的数量关系,并证明你的结论.
分析 ①由SAS证明△ACD≌△AEB,得出对应边相等即可;
②在PD上截取PM=PA,连接AM,同(1)得:△ACD≌△AEB,得出∠ADC=∠ABE,得出A、D、B、P四点共圆,由圆周角定理得出∠APD=∠ABD,证出△ABD是等边三角形,得出∠ABD=60°,得出△APM是等边三角形,因此AM=PA,由AAS证明△ADM≌△ABP,得出MD=PB,即可得出结论;
③由等腰直角三角形的性质得出∠ABD=45°=∠BAC,证出BD∥AC,同理:AB∥CE,得出∠BCD=∠BNC,同①得:A、D、B、P四点共圆,由圆周角定理得出∠BDP=∠BAP=30°,由三角形的外角性质得出∠BNC=75°,得出∠BCD=75°,再由三角形内角和定理求出∠DBC=∠BCD,即可得出结论.
解答 ①证明:∵∠BAD=∠EAC,
∴∠DAC=∠BAE,
在△ACD和△AEB中,$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠DAC=∠BAE}&{\;}\\{AC=AE}&{\;}\end{array}\right.$,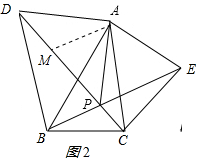 ∴△ACD≌△AEB(SAS),
∴△ACD≌△AEB(SAS),
∴CD=BE;
②证明:在PD上截取PM=PA,连接AM,如图2所示:
同(1)得:△ACD≌△AEB,
∴∠ADC=∠ABE,
∴A、D、B、P四点共圆,
∴∠APD=∠ABD,
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠APD=60°,
∴△APM是等边三角形,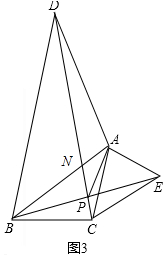
∴AM=PA,∠PAM=60°,
∴∠DAM=∠BAP,
在△ADM和△ABP中,$\left\{\begin{array}{l}{∠DAM=∠BAP}&{\;}\\{∠ADM=∠ABP}&{\;}\\{AM=AP}&{\;}\end{array}\right.$,
∴△ADM≌△ABP(AAS),
∴MD=PB,
∴PM+MD=PA+PB,
即PD=PA+PB;
③解:BD=CD,理由如下:
∵∠BAD=90°,AB=AD,
∴∠ABD=45°=∠BAC,
∴BD∥AC,同理:AB∥CE,
∴∠BCD=∠BNC,
同①得:A、D、B、P四点共圆,
∴∠BDP=∠BAP=30°,
∴∠BNC=30°+45°=75°,
∴∠BCD=75°,
∴∠DBC=180°-75°-30°=75°=∠BCD,
∴BD=CD.
点评 本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的性质、等边三角形的判定与性质、三角形内角和定理、四点共圆、圆周角定理等知识;证明三角形全等是解决问题的关键.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案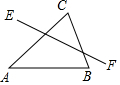 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )| A. | 4$\sqrt{6}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
 如图,这是一个4×7的正方形网格,则图中一共有60个正方形,一共有280个长方形.
如图,这是一个4×7的正方形网格,则图中一共有60个正方形,一共有280个长方形. 已知三条直线AB,CD,EF相交于同一点O,若∠AOE=2∠AOC,∠COF比∠AOE大30°,则∠BOD的度数是多少?
已知三条直线AB,CD,EF相交于同一点O,若∠AOE=2∠AOC,∠COF比∠AOE大30°,则∠BOD的度数是多少?