题目内容
12.(1)求值:|$\sqrt{3}$-2|+20090-(-$\frac{1}{3}$)-1+3tan30°(2)先化简,再求值:($\frac{x-1}{x}$-$\frac{x-2}{x+1}$)÷$\frac{2{x}^{2}-x}{{x}^{2}+2x+1}$,其中x=$\sqrt{2}$.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原式=2-$\sqrt{3}$+1+3+$\sqrt{3}$=6;
(2)原式=$\frac{{x}^{2}-1-{x}^{2}+2x}{x(x+1)}$•$\frac{x(2x-1)}{(x+1)^{2}}$=$\frac{2x-1}{x(x+1)}$•$\frac{(x+1)^{2}}{x(2x-1)}$=$\frac{x+1}{{x}^{2}}$,
当x=$\sqrt{2}$时,原式=$\frac{\sqrt{2}+1}{2}$.
点评 此题考查了实数的运算,以及分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.九年级(1)班体检结果出来后,一位同学对全班同学的身高(单位:厘米)统计如表:
这组数据的众数为( )
| 身高(厘米) | 158 | 160 | 162 | 165 | 167 | 170 |
| 人数 | 2 | 5 | 8 | 18 | 10 | 7 |
| A. | 158 | B. | 162 | C. | 165 | D. | 167 |
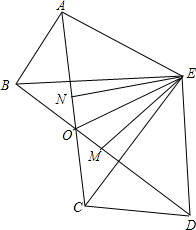 如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证:
如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证: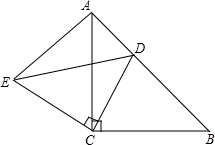 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,