题目内容
4.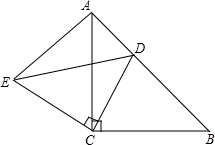 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,(1)求证:△ACE≌△BCD;
(2)若AE=3,AD=2,求DE的长度.
分析 (1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD.
(2)由(1)的论证结果得出∠DAE=90°,利用勾股定理得出答案即可.
解答 (1)证明:∵∠ACB=∠ECD=90°,
∴∠ACD+∠BCD=∠ACD+∠ACE,
即∠BCD=∠ACE.
∵BC=AC,DC=EC,
∴△ACE≌△BCD.
(2)解:∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45°,
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
即DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{13}$.
点评 本题考查三角形全等的判定与性质,等腰直角三角形的性质,及勾股定理的运用,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | 3a2-a2=3 | B. | a6÷a2=a3 | C. | (a2)3=a5 | D. | a2•a3=a5 |
9.到2006年2月中旬,黄河干流龙羊峡、小浪底等五大水库蓄水总量达347.4亿立方米,创1996年以来蓄水新高,为农业春灌储备了较为充足的水源.其中347.4亿用科学记数法表示应为( )
| A. | 0.3474×1011 | B. | 3.474×1010 | C. | 34.74×109 | D. | 3.474×1011 |
14.下列计算正确的是( )
| A. | 2m+3n=5mn | B. | m2•m3=m6 | C. | m8÷m6=m2 | D. | (-m)3=m3 |
 如图,AC为一根电线杆,钢缆AB的长为5m,钢缆底端B与电线底端C的距离为3m,在D处有一个蜘蛛窝.两只蜘蛛同时从点D出发以同样的速度沿路径D-A-B和路径D-C-B织网,结果正好在点B相遇,求蜘蛛窝D的高度.
如图,AC为一根电线杆,钢缆AB的长为5m,钢缆底端B与电线底端C的距离为3m,在D处有一个蜘蛛窝.两只蜘蛛同时从点D出发以同样的速度沿路径D-A-B和路径D-C-B织网,结果正好在点B相遇,求蜘蛛窝D的高度.