题目内容
如图多边形ABCDEFGH相邻两边互相垂直，若要求出其周长，则所需知最少边数是（ ）| A、3 | B、4 | C、5 | D、6 |
考点：平移的性质
专题：数形结合
分析：根据平移的性质，可将AH、GF、ED的和转化为线段BC的长度，然后需要知道AB、BC、EF的长度，可求出它的周长．
解答：解：知道：AB、BC和EF三条边就能计算其周长
根据平移的性质，可将AH、GF、ED的和转化为线段BC的长度，HN、CD即是AB的长度，
GN=EF，
∴周长为：AB+BC+CD+DE+EF+GH+AH=2AB+2BC+2EF．
故所需知道的最少边数为3．
故选A．
根据平移的性质，可将AH、GF、ED的和转化为线段BC的长度，HN、CD即是AB的长度，
GN=EF，
∴周长为：AB+BC+CD+DE+EF+GH+AH=2AB+2BC+2EF．
故所需知道的最少边数为3．
故选A．
点评：本题主要考查了平移的性质，属于基础应用题目，难度不大，把不规则图形部分平移到规则图形的部分是解题的关键．
练习册系列答案
相关题目
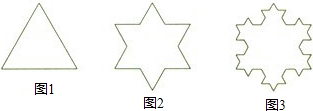
我们来探究“雪花曲线”的有关问题：如图1是长为1的正三角形，现将它作如下变换：取三角形各边的三等分点向形外作没有底边的等边三角形，这样得到一个六角星（如图2）；继续对六角星各边施行相同的变换，得到“雪花形”（如图3）．如此继续下去，第4次变换后得到的图形的周长应等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，奥运五环标志里，包含了圆与圆位置关系中的（ ）| A、相切，内含 |
| B、外切，内含 |
| C、外离，相交 |
| D、相切，相交 |
在∠AOB的角平分线上有一点P，在OA上有一点M，在OB上有一点N，若PM=PN，则△POM与△PON（ ）
| A、一定全等 | B、可能全等 |
| C、一定不全等 | D、无法确定 |
礼堂第一排有a个座位，后面每排多1个座位，礼堂共有15排座位，则这礼堂的座位总数有（ ）个．
| A、15a+105 |
| B、15a+136 |
| C、15a+120 |
| D、14a+105 |
如果a是方程x2+bx+a=0的根，a≠0，则a+b等于（ ）
A、-
| ||
| B、-1 | ||
C、
| ||
| D、1 |
若实数x、y满足（x+y+3）（x+y-1）=0，则x+y的值为（ ）
| A、1 | B、-3 |
| C、3或-1 | D、-3或1 |
若ab≠1，且有a2+2010a+6=0及6b2+2010b+1=0，则
的值是（ ）
| a |
| b |
| A、6 | ||
B、
| ||
| C、2010 | ||
D、
|