题目内容
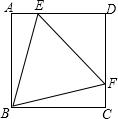 如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( )
如图,正方形ABCD中,AB=4,点E,F分别在AD,DC上,且△BEF为等边三角形,则△EDF与△BFC的面积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、5:3 |
考点:正方形的性质,等边三角形的性质
专题:
分析:根据正方形的性质可得AB=BC,∠A=∠C=90°,根据等边三角形的性质可得BE=BF,然后利用“HL”证明Rt△ABE和Rt△CBF全等,根据全等三角形对应边相等可得AE=CF,然后求出DE=DF,从而得到△DEF是等腰直角三角形,设DE=DF=x,表示出EF、CF,然后在Rt△BCF中利用勾股定理列出方程表示出x2,然后表示出S△EDF和S△BFC,求解即可.
解答:解:在正方形ABCD中,AB=BC,∠A=∠C=90°,
∵△BEF为等边三角形,
∴BE=BF,
在Rt△ABE和Rt△CBF中,
,
∴Rt△ABE≌Rt△CBF(HL),
∴AE=CF,
∴AD-AE=CD-CF,
即DE=DF,
∴△DEF是等腰直角三角形,
设DE=DF=x,则EF=
x,CF=4-x,
在Rt△BCF中,BC2+CF2=BF2,
即42+(4-x)2=(
x)2,
整理得,x2=8(4-x),
∵S△EDF=
x2=4(4-x),
S△BFC=
×4(4-x),
∴△EDF与△BFC的面积比为2:1.
故选A.
∵△BEF为等边三角形,
∴BE=BF,
在Rt△ABE和Rt△CBF中,
|
∴Rt△ABE≌Rt△CBF(HL),
∴AE=CF,
∴AD-AE=CD-CF,
即DE=DF,
∴△DEF是等腰直角三角形,
设DE=DF=x,则EF=
| 2 |
在Rt△BCF中,BC2+CF2=BF2,
即42+(4-x)2=(
| 2 |
整理得,x2=8(4-x),
∵S△EDF=
| 1 |
| 2 |
S△BFC=
| 1 |
| 2 |
∴△EDF与△BFC的面积比为2:1.
故选A.
点评:本题考查了正方形的性质,等边三角形的性质,全等三角形的判定与性质,关键在于求出△DEF是等腰直角三角形,难点在于分别表示出两个三角形的面积.

练习册系列答案
相关题目
下列各点中,在函数y=2x-6的图象上的是( )
| A、(-2,3) |
| B、(3,-2) |
| C、(1,4) |
| D、(4,2) |
若二次函数f(x)=ax2+bx+c的对称轴为x=1,且其图象过点(2,0),则
的值是( )
| f(-1) |
| f(1) |
| A、-3 | B、-2 | C、2 | D、3 |
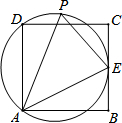 如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )
如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )A、10
| ||
B、10
| ||
| C、32 | ||
D、5
|
 如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;
如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;