题目内容
如图,△OBD和△OCA是等腰直角三角形,∠ODB=∠OCA=90°.M是线段AB中点,连接DM、CM、CD.若C在直线OB上,试判断△CDM的形状.


考点:等腰直角三角形,直角三角形斜边上的中线
专题:几何综合题
分析:由△OBD和△OCA是等腰直角三角形得到∠ACB=∠ADB=90°,∠OBD=45°,由M为AB的中点,根据直角三角形斜边上的中线性质得到DM=AM=BM,CM=AM=BM,则CM=DM,∠MBD=∠MDB,∠MCB=∠MBC,理由三角形外角性质得∠AMD=2∠MBD,∠AMC=2∠MBC,则∠AMD-∠AMC=2(∠MBD-∠MBC)=2∠OBD=90°,于是可得到△CDM为等腰直角三角形.
解答:解:△CDM为等腰直角三角形.理由如下:
∵△OBD和△OCA是等腰直角三角形,
∴∠ACB=∠ADB=90°,∠OBD=45°,
而M为AB的中点,
∴DM=AM=BM,CM=AM=BM,
∴CM=DM,∠MBD=∠MDB,∠MCB=∠MBC,
∴∠AMD=2∠MBD,∠AMC=2∠MBC,
∴∠AMD-∠AMC=2(∠MBD-∠MBC)=2∠OBD=90°,
即∠CMD=90°,
∵CM=DM,
∴△CDM为等腰直角三角形.
∵△OBD和△OCA是等腰直角三角形,
∴∠ACB=∠ADB=90°,∠OBD=45°,
而M为AB的中点,
∴DM=AM=BM,CM=AM=BM,
∴CM=DM,∠MBD=∠MDB,∠MCB=∠MBC,
∴∠AMD=2∠MBD,∠AMC=2∠MBC,
∴∠AMD-∠AMC=2(∠MBD-∠MBC)=2∠OBD=90°,
即∠CMD=90°,
∵CM=DM,
∴△CDM为等腰直角三角形.
点评:本题考查了等腰直角三角形的性质和直角三角形斜边上的中线性质、三角形外角的性质,灵活利用直角三角形的斜边上的中线的性质是关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
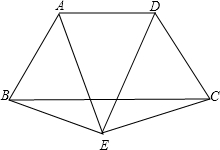 如图所示,在等腰梯形ABCD中,AB=CD,AD∥BC,点E是梯形外的一点,且EA=ED,若点F是BC的中点,试判断EF与BC的位置关系,并说明理由.
如图所示,在等腰梯形ABCD中,AB=CD,AD∥BC,点E是梯形外的一点,且EA=ED,若点F是BC的中点,试判断EF与BC的位置关系,并说明理由. 已知如图,抛物线
已知如图,抛物线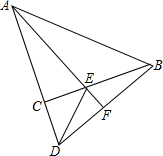 如图,△ABC和△CDE都是等腰三角形,且A、C、D三点共线,E是BC上一点,AE的延长线与BD相交于点F.
如图,△ABC和△CDE都是等腰三角形,且A、C、D三点共线,E是BC上一点,AE的延长线与BD相交于点F.  在平面直角坐标系中,已知A(-1,-1),B(1,-3),C(2,0)
在平面直角坐标系中,已知A(-1,-1),B(1,-3),C(2,0)