Question

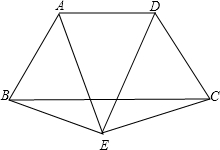如图所示，在等腰梯形ABCD中，AB=CD，AD∥BC，点E是梯形外的一点，且EA=ED，若点F是BC的中点，试判断EF与BC的位置关系，并说明理由．

Answer 1

考点：等腰梯形的性质

专题：

分析：根据等腰梯形的性质求出∠BAD=∠CDA，根据等腰三角形的性质得出∠EAD=∠EDA，求出∠BAE=∠CDE，证△BAE≌△CDE，推出BE=CE即可．

解答：解：EF⊥BC，
理由是：∵在等腰梯形ABCD中，AB=CD，AD∥BC，
∴∠BAD=∠CDA，
∵AE=DE，
∴∠EAD=∠EDA，
∴∠BAD-∠EAD=∠CDA-∠EDA，
∴∠BAE=∠CDE，
在△BAE和△CDE中

AB=DC ∠BAE=∠CDE AE=DE

∴△BAE≌△CDE，
∴BE=CE，
∵F为BC的中点，
∴EF⊥BC．

点评：本题考查了等腰梯形的性质，等腰三角形的性质，全等三角形的性质和判定的应用，主要考查学生的推理能力．