Question

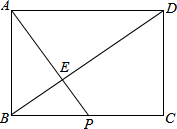
梯形ABCD中，AD∥BC，延长BD至E，连接AE、CE，有BE=BC，AE=CD，∠DCB=∠AED，作BF⊥CE于F，求证：
（1）∠EBF=∠CBF；
（2）△EBC是等边三角形．

Answer 1

考点：全等三角形的判定与性质,等边三角形的判定与性质,梯形

专题：证明题

分析：（1）根据等腰三角形的性质推出即可；
（2）证ABE≌△DBC，推出∠ABE=∠DBC，BD=AB，求出AB=BD，推出AB=BD=AD，得出△ABD是等边三角形，求出∠EBC=∠ABE=60°，根据等边三角形的判定得出即可．

解答：证明：（1）∵BE=BC，BF⊥CE，
∴∠EBF=∠CBF（三线合一）；

（2）在△ABE与△DBC中，

AE=DC ∠AEB=∠BCD BE=BC

，
∴△ABE≌△DBC（SAS，
∴∠ABE=∠DBC，BD=AB，
∵AD∥BC，
∴∠ADB=∠DBC，
∵∠ADB=∠ABD，
∴AB=BD，
∴AB=BD=AD，
∴△ABD是等边三角形，
∴∠ABD=60°，
∴∠EBC=∠ABE=60°，
∵BE=BC，
∴△EBC是等边三角形．

点评：本题考查了等边三角形的判定，平行线的性质，全等三角形的性质和判定，等腰三角形的性质和判定的应用，主要考查学生的推理能力．