题目内容
游泳者在河中逆流而上,所带水壶于桥A下被水冲走,继续向前游了20分钟他发现水壶遗失,于是立即返回,在桥A下游2千米处的B桥下追到水壶,求该河流的水流速度.
考点:分式方程的应用
专题:
分析:如果设该河水流的速度是每小时x千米,游泳者在静水中每小时游a千米.那么游泳者自桥A逆流游了
(a-x)千米,他再返回追到水壶用了
小时,这个时间比水壶在遗失后漂流时间
小时少
小时.由此列出方程,求得问题的解.
| 1 |
| 3 |
2+
| ||
| a+x |
| 2 |
| x |
| 1 |
| 3 |
解答:解:解:设该河水流的速度是每小时x千米,游泳者在静水中每小时游a千米.由题意,
得
=
-
,
解得:x=3.
经检验,x=3是原方程的解.
答:这条河的水流速度为3千米/小时.
得
2+
| ||
| a+x |
| 2 |
| x |
| 1 |
| 3 |
解得:x=3.
经检验,x=3是原方程的解.
答:这条河的水流速度为3千米/小时.
点评:此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.注意不要忘记检验.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
若x1,x2是一元二次方程x2-x-1=0的两根,则x1x2的值是( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|

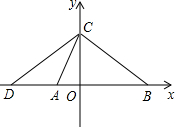 如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点C,过点C与AC垂直的直线交x轴于点B,在x轴负半轴上取一点D,使AD=OC,连接CD.
如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点C,过点C与AC垂直的直线交x轴于点B,在x轴负半轴上取一点D,使AD=OC,连接CD.