题目内容
 如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED证明:∵BE=FC
∴BE+EF=FC+EF(
即:
∵AB∥CD
∴∠B=∠C(
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE(
∴∠AFB=∠DEC(
∴AF∥ED(
考点:全等三角形的判定与性质
专题:推理填空题
分析:由BE=CF,利用等式的性质得到BF=CE,再由AB与DC平行,得到两对内错角相等,利用AAS得到三角形ABF与三角形DCE全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答:证明:∵BE=FC,
∴BE+EF=FC+EF(等式的性质),
即BF=CE,
∵AB∥CD,
∴∠B=∠C(两直线平行内错角相等),
∠A=∠D,
∠B=∠C,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴∠AFB=∠DEC(全等三角形对应角相等),
∴AF∥ED(内错角相等两直线平行).
故答案为:等式的性质;BF=CE;两直线平行内错角相等;AAS;全等三角形对应角相等;内错角相等两直线平行
∴BE+EF=FC+EF(等式的性质),
即BF=CE,
∵AB∥CD,
∴∠B=∠C(两直线平行内错角相等),
∠A=∠D,
∠B=∠C,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(AAS),
∴∠AFB=∠DEC(全等三角形对应角相等),
∴AF∥ED(内错角相等两直线平行).
故答案为:等式的性质;BF=CE;两直线平行内错角相等;AAS;全等三角形对应角相等;内错角相等两直线平行
点评:此题考查了全等三角形的判定与性质,以及平行线的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
| A、a的系数是0 | ||
B、
| ||
| C、0是单项式 | ||
| D、-5y的系数是5 |

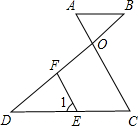 已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.