题目内容
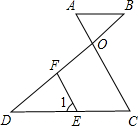已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A．（1）求证：FE∥OC；
（2）若∠B=40°，∠1=60°，求∠OFE的度数．
考点：平行线的判定与性质,三角形的外角性质
专题：
分析：（1）根据平行线的性质和已知得出∠1=∠C，根据平行线的判定推出即可；
（2）根据平行线的性质求出∠D，根据三角形的外角性质推出即可．
（2）根据平行线的性质求出∠D，根据三角形的外角性质推出即可．
解答：（1）证明：∵AB∥DC，
∴∠A=∠C，
∵∠1=∠A，
∴∠1=∠C，
∴FE∥OC；
（2）解：∵AB∥DC，
∴∠D=∠B，
∵∠B=40°
∴∠D=40°，
∵∠OFE是△DEF的外角，
∴∠OFE=∠D+∠1，
∵∠1=60°，
∴∠OFE=40°+60°=100°．
∴∠A=∠C，
∵∠1=∠A，
∴∠1=∠C，
∴FE∥OC；
（2）解：∵AB∥DC，
∴∠D=∠B，
∵∠B=40°
∴∠D=40°，
∵∠OFE是△DEF的外角，
∴∠OFE=∠D+∠1，
∵∠1=60°，
∴∠OFE=40°+60°=100°．
点评：本题考查了平行线的性质和判定，三角形的内角和定理的应用，主要考查学生的推理能力和计算能力，题目比较好，难度适中．
练习册系列答案
相关题目
如图，由∠1=∠2，∠D=∠B，推出以下结论，其中错误的是（ ）| A、AB∥DC |
| B、AD∥BC |
| C、∠DAB=∠BCD |
| D、∠DCA=∠DAC |
如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（ ）| A、两点之间的线段最短 |
| B、长方形的四个角都是直角 |
| C、长方形是轴对称图形 |
| D、三角形有稳定性 |
如图，已知：点B、E、F、C在同一直线上，∠A=∠D，BE=CF，且AB∥CD．求证：AF∥ED