题目内容
20.若一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1、x2,则两根与方程系数之间有如下关系:x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$
根据上述材料计算:
已知x1、x2是方程x2+4x+2=0的两个实数根,求下列代数式的值.
(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$
(2)x12+x22
(3)(x1-1)(x2-1)
分析 根据x1、x2是方程x2+4x+2=0的两个实数根,求出x1+x2,x1•x2的值,再根据(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,(2)x12+x22=(x1+x2)2-2x1x2);(3)(x1-1)(x2-1)=x1x2-(x1+x2)+1即可求出答案.
解答 解:∵x1、x2是方程x2+4x+2=0的两个实数根,
∴x1+x2=-4,x1•x2=2,
∴(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-4}{2}$=-2;
(2)x12+x22=(x1+x2)2-2x1x2=16-4=12;
(3)(x1-1)(x2-1)=x1x2-(x1+x2)+1=2-(-4)+1=7.
点评 此题考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
9.Rt△ABC中,∠C=90°,tanA=$\frac{3}{5}$,BC=5,则AB=( )
| A. | 3 | B. | 4 | C. | $\frac{25}{3}$ | D. | $\frac{5\sqrt{34}}{3}$ |
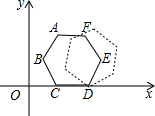 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.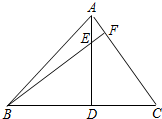 已知在△ABC中,AD⊥BC,垂足D点在边BC上,BF⊥AC分别交射线DA、射线CA于点E、F,若BD=4,∠BAD=45°.
已知在△ABC中,AD⊥BC,垂足D点在边BC上,BF⊥AC分别交射线DA、射线CA于点E、F,若BD=4,∠BAD=45°.