题目内容
10.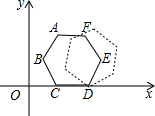 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.
分析 根据C、D的坐标分别为(1,0)和(2,0),得到正六边形ABCDEF的边长为1,根据正六边形的性质得到∠A=∠B=∠C=∠D=∠E=∠F=120°,求得∠CED=30°,过D作DH⊥CE于H,解直角三角形得到EH=$\frac{\sqrt{3}}{2}$,CE=$\sqrt{3}$,同理CF=2,AC=$\sqrt{3}$,当点C第一次回到x轴上时,点C经过的路线长为$\frac{60π×1}{180}$+$\frac{60π×\sqrt{3}}{180}$+$\frac{60π×2}{180}$+$\frac{60π×\sqrt{3}}{180}$+$\frac{60π×1}{180}$=$\frac{4+2\sqrt{3}}{3}$π,当点C第三次回到x轴上时,点C经过的路线长(4+2$\sqrt{3}$)π,
解答 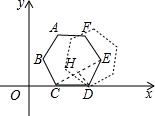 解:∵C、D的坐标分别为(1,0)和(2,0),
解:∵C、D的坐标分别为(1,0)和(2,0),
∴正六边形ABCDEF的边长为1,
∵∠A=∠B=∠C=∠D=∠E=∠F=120°,
∴∠CED=30°,
过D作DH⊥CE于H,
∴EH=$\frac{\sqrt{3}}{2}$,
∴CE=$\sqrt{3}$,
同理CF=2,AC=$\sqrt{3}$,
∴当点C第一次回到x轴上时,
∴点C经过的路线长为$\frac{60π×1}{180}$+$\frac{60π×\sqrt{3}}{180}$+$\frac{60π×2}{180}$+$\frac{60π×\sqrt{3}}{180}$+$\frac{60π×1}{180}$=$\frac{4+2\sqrt{3}}{3}$π,
当点C第三次回到x轴上时,点C经过的路线长(4+2$\sqrt{3}$)π.
故答案为:(4+2$\sqrt{3}$)π.
点评 本题考查的是正多边形和圆及图形旋转的性质,弧长的计算,坐标与图形的性质,正确的识图是解答此题的关键.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 2x+3x=5 | B. | 2x+3x=6x | C. | 2x+3x=5x2 | D. | 2x+3x=5x |
| A. | $\sqrt{4-x}$有意义,则x≥4 | B. | 2x2-7在实数范围内不能因式分解 | ||
| C. | 方程x2+1=0无解 | D. | 方程x2=2x的解为 $x=±\sqrt{2x}$ |
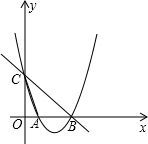 如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c经过B、C两点,且与x轴的另一个交点为A,连接AC.
如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c经过B、C两点,且与x轴的另一个交点为A,连接AC.
