题目内容
9.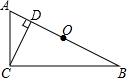 如图,已知在△ABC中,O为AB的中点,∠ACB=90°,CD⊥AB于D,CD=5,DO=$\sqrt{11}$,求S△ABC.
如图,已知在△ABC中,O为AB的中点,∠ACB=90°,CD⊥AB于D,CD=5,DO=$\sqrt{11}$,求S△ABC.
分析 连结CO,先由勾股定理求出OC的长,再根据直角三角形斜边上的中线等于斜边的一半得出AB=2OC,然后利用S△ABC=$\frac{1}{2}$AB•CD计算即可求解.
解答 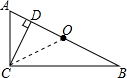 解:连结CO,
解:连结CO,
在△ODC中,∵∠ODC=90°,CD=5,DO=$\sqrt{11}$,
∴OC=$\sqrt{C{D}^{2}+D{O}^{2}}$=$\sqrt{{5}^{2}+(\sqrt{11})^{2}}$=6,
∵在△ABC中,O为AB的中点,∠ACB=90°,
∴AB=2OC=12,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×12×5=30.
点评 本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.也考查了勾股定理与三角形的面积,准确作出辅助线是解题的关键.

练习册系列答案
相关题目
19.若方程$\frac{A}{x-3}$+$\frac{B}{x+4}$=$\frac{2x+1}{(x-3)(x+4)}$,则A、B的值分别为( )
| A. | 2,1 | B. | 1,2 | C. | 1,1 | D. | -1,-1 |
4.依法纳税是公民应尽的义务,2006年,我国个人所得税规定,全民全月工薪,薪金所得不超过1000元不必纳税,超过1000元的部分为全月应纳税所得额,此项税款按下表累加计算:
小明妈妈2006年3月纳税135元,她本人的工薪收入为多少元?
| 全月应纳税所得额 | 税率 |
| 不超过500元 | 5% |
| 超过500元至2000元部分 | 10% |
| 超过2000元至5000元部分 | 15% |
| … | … |
 在?ABCD中,EG∥BC,点E在AC上,点G在BD上,且EF⊥CD于F,GH⊥AB于H,求证:GH=EF.
在?ABCD中,EG∥BC,点E在AC上,点G在BD上,且EF⊥CD于F,GH⊥AB于H,求证:GH=EF.