题目内容
已知P为⊙O的直径DC延长线上一点,过点P作⊙O的切线PA、PB,切点为A、B,连接AB交PO于E,过D作DF⊥PA延长线于F,连AC、EF、BD.则下列结论正确的是 .
①C为△PAB内心;②AC⊥EF;③AB=2AF;④BD为△PAB外接圆切线.
①C为△PAB内心;②AC⊥EF;③AB=2AF;④BD为△PAB外接圆切线.
考点:圆的综合题
专题:
分析:连接AD,BC,根据切线的性质,得出PA=PB,∠APD=∠BPD,根据等腰三角形的性质得出PE⊥AB,AB=2AE,通过△APD≌△BPD得出∠ADC=∠BDC,根据圆周角的性质得出
=
,进而得出∠BAC=∠ABC,根据圆周角和弦切角的性质得出∠PAC=∠ABC,即可得出AC是∠PAB的平分线,BC是∠PBA的平分线,从而确定C为△PAB内心,故①正确;
根据直径所对的角是直角,得出AD⊥AC,由于AD与EF相交,所以AC不会垂直于EF,故②错误;
根据弦切角的性质以及互为余角的性质得出AD是∠PDF的平分线,根据角平分线的性质即可得出AE=AF,进而得出AB=2AF,故③正确;
由于BC⊥BD,C为△PAB内心,只有C同时也是外心才能判定BD为△PAB外接圆切线,即△PAB是等边三角形,由于不能求得是等边三角形,故④错误.
 |
| AC |
 |
| BC |
根据直径所对的角是直角,得出AD⊥AC,由于AD与EF相交,所以AC不会垂直于EF,故②错误;
根据弦切角的性质以及互为余角的性质得出AD是∠PDF的平分线,根据角平分线的性质即可得出AE=AF,进而得出AB=2AF,故③正确;
由于BC⊥BD,C为△PAB内心,只有C同时也是外心才能判定BD为△PAB外接圆切线,即△PAB是等边三角形,由于不能求得是等边三角形,故④错误.
解答: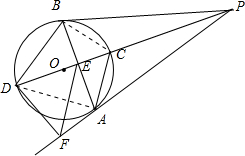 解:连接AD,BC,
解:连接AD,BC,
∵过点P作⊙O的切线PA、PB,切点为A、B,
∴PA=PB,
∴∠APD=∠BPD,
∴PE⊥AB,AB=2AE,
在△APD和△BPD中,
,
∴△APD≌△BPD(SAS),
∴∠ADC=∠BDC,
∴
=
,
∴∠BAC=∠ABC,
∵PA、PB是切线,
∴∠PAC=∠ABC,
∴∠PAC=∠BAC,
∴AC是∠PAB的平分线,
同理,BC是∠PBA的平分线,
∴C为△PAB内心,故①正确;
∵DC是直径,
∴AD⊥AC,
∵AD与EF相交,
∴AC不会垂直于EF,故②错误;
∵∠PAC=∠ADC,∠DAC=90°,
∴∠DAF+∠PAC=90°,
∴∠ADC+∠DAF=90°,
∵DF⊥PA,
∴∠ADF+∠DAF=90°,
∴∠ADC=∠ADF,
∴AE=AF,
∴AB=2AF,故③正确;
∵CD是直径,
∴CB⊥BD,
要使BD为△PAB外接圆切线,BC必经过△PAB外接圆的圆心,
∵PD垂直平分AB,
∴点C即为三角形的外心,
∵C为△PAB内心,
∵不能确定△PAB是等边三角形,
∴BD为△PAB外接圆切线不能确定,故④错误.
故答案为①③.
 解:连接AD,BC,
解:连接AD,BC,∵过点P作⊙O的切线PA、PB,切点为A、B,
∴PA=PB,
∴∠APD=∠BPD,
∴PE⊥AB,AB=2AE,
在△APD和△BPD中,
|
∴△APD≌△BPD(SAS),
∴∠ADC=∠BDC,
∴
 |
| AC |
 |
| BC |
∴∠BAC=∠ABC,
∵PA、PB是切线,
∴∠PAC=∠ABC,
∴∠PAC=∠BAC,
∴AC是∠PAB的平分线,
同理,BC是∠PBA的平分线,
∴C为△PAB内心,故①正确;
∵DC是直径,
∴AD⊥AC,
∵AD与EF相交,
∴AC不会垂直于EF,故②错误;
∵∠PAC=∠ADC,∠DAC=90°,
∴∠DAF+∠PAC=90°,
∴∠ADC+∠DAF=90°,
∵DF⊥PA,
∴∠ADF+∠DAF=90°,
∴∠ADC=∠ADF,
∴AE=AF,
∴AB=2AF,故③正确;
∵CD是直径,
∴CB⊥BD,
要使BD为△PAB外接圆切线,BC必经过△PAB外接圆的圆心,
∵PD垂直平分AB,
∴点C即为三角形的外心,
∵C为△PAB内心,
∵不能确定△PAB是等边三角形,
∴BD为△PAB外接圆切线不能确定,故④错误.
故答案为①③.
点评:本题考查了切线的性质,圆周角,弦切角的性质,三角形全等的判定和性质,熟练掌握性质和定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
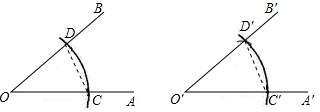 请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
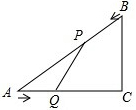 已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题:
已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题: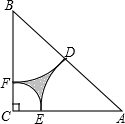 如图,在Rt△ABC中,∠C=90°,BC=AC=2cm,分别以A,C,B为圆心作弧,使
如图,在Rt△ABC中,∠C=90°,BC=AC=2cm,分别以A,C,B为圆心作弧,使
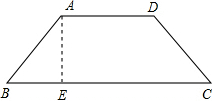 如图,铁路路基的横截面是等腰梯形,斜坡AB的坡度为1:
如图,铁路路基的横截面是等腰梯形,斜坡AB的坡度为1: