题目内容
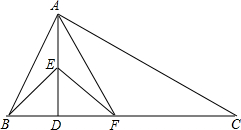 如图,在△ABC中,∠BAC=90°,AD是斜边BC上的高,∠ABD的平分线交AD于点E,∠CAD的平分线交CD于点F,连接EF.求证:EF∥AC.
如图,在△ABC中,∠BAC=90°,AD是斜边BC上的高,∠ABD的平分线交AD于点E,∠CAD的平分线交CD于点F,连接EF.求证:EF∥AC.考点:平行线分线段成比例
专题:证明题
分析:根据角平分线定理得到
=
和
=
,再证明Rt△ABD∽Rt△CAD得到
=
,利用比例性质得
=
,则
=
,然后根据平行线分线段成比例定理的逆定理可得EF∥AC.
| AE |
| DE |
| BA |
| BD |
| CF |
| DF |
| AC |
| AD |
| BA |
| AC |
| BD |
| AD |
| BA |
| BD |
| AC |
| AD |
| AE |
| DE |
| CF |
| DF |
解答:解:∵∠ABD的平分线交AD于点E,
∴
=
,
∵∠CAD的平分线交CD于点F,
∴
=
,
∵AD是斜边BC上的高,
∴∠ADB=∠ADC=90°,
∴∠ABD+∠BAD=90°,
而∠BAD+∠CAD=90°,
∴∠ABD=∠CAD,
∴Rt△ABD∽Rt△CAD,
∴
=
,
∴
=
,
∴
=
,
∴EF∥AC.
∴
| AE |
| DE |
| BA |
| BD |
∵∠CAD的平分线交CD于点F,
∴
| CF |
| DF |
| AC |
| AD |
∵AD是斜边BC上的高,
∴∠ADB=∠ADC=90°,
∴∠ABD+∠BAD=90°,
而∠BAD+∠CAD=90°,
∴∠ABD=∠CAD,
∴Rt△ABD∽Rt△CAD,
∴
| BA |
| AC |
| BD |
| AD |
∴
| BA |
| BD |
| AC |
| AD |
∴
| AE |
| DE |
| CF |
| DF |
∴EF∥AC.
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了角平分线定理和相似三角形的判定与性质.

练习册系列答案
相关题目
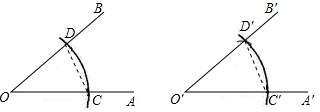 请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
 如图,△AOB为等腰三角形,顶点A的坐标(2,
如图,△AOB为等腰三角形,顶点A的坐标(2,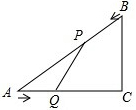 已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题:
已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题: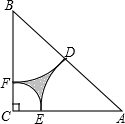 如图,在Rt△ABC中,∠C=90°,BC=AC=2cm,分别以A,C,B为圆心作弧,使
如图,在Rt△ABC中,∠C=90°,BC=AC=2cm,分别以A,C,B为圆心作弧,使