题目内容
如图所示，将△AOB绕着点O旋转180度得到△DOC．过点O的一条直线分别交BA、CD的延长线于点E、F．求证：AE=DF．考点：旋转的性质,全等三角形的判定与性质
专题：证明题
分析：根据旋转的性质可得到点A、O、D共线，点B、O、C三点在一条直线上，∠B=∠C，OA=OC，则可判断AB∥CD，得到∠E=∠F，然后根据“AAS”可判断△OAE≌△ODF，所以AE=DF．
解答：证明：∵△AOB绕着点O旋转180度得到△DOC，
∴点A、O、D共线，点B、O、C三点在一条直线上，∠B=∠C，OA=OC，
∴AB∥CD，
∴∠E=∠F，
在△OAE和△ODF中，
，
∴△OAE≌△ODF（AAS），
∴AE=DF．
∴点A、O、D共线，点B、O、C三点在一条直线上，∠B=∠C，OA=OC，
∴AB∥CD，
∴∠E=∠F，
在△OAE和△ODF中，
|
∴△OAE≌△ODF（AAS），
∴AE=DF．
点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
相关题目
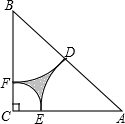如图，在Rt△ABC中，∠C=90°，BC=AC=2cm，分别以A，C，B为圆心作弧，使
