题目内容
3.平行四边形ABCD中,AC、BD相交于点O,AB=16,4C=24,BD=40,则△AOB的周长是48.分析 根据平行四边形性质推出OA=OC,OB=OD,求出AO、OB,即可求出答案.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC,OD=OB=$\frac{1}{2}$BD,
∵4C=24,BD=40,
∴OA=12,OB=20,
∵AB=16,
∴△AOB的周长是AB+OA+OB=16+12+20=48,
故答案为:48.
点评 本题主要考查对平行四边形性质的理解和掌握,能熟练地运用性质求出OA、OB的长是解此题的关键,注意:平行四边形的对角线互相平分.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | b3•b3=2b3 | B. | $\sqrt{{2}^{2}}$=±2 | C. | (a4)2÷a2=a6 | D. | $\root{3}{-27}$=3 |
18.将两个不等边的全等三角形纸片,在桌面上用各种不同的方法拼四边形,在这些拼成的四边形中,是平行四边形的共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.小亮问老师有多少岁了,老师说:“我像你这么大时,你才4岁,你到我这么大时,我就40岁了.”求小亮和老师的岁数各是多少?若设小亮和老师的岁数分别为x岁和y岁,则可列方程组( )
| A. | $\left\{\begin{array}{l}{x-4=y-x}\\{y-x=40-y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=4}\\{x+y=40}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-4=y}\\{y-40=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-4=x-y}\\{y-x=y-40}\end{array}\right.$ |
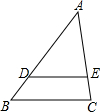 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=9,则AB等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=9,则AB等于( )