题目内容
1.菱形ABCD中,∠A=60°,AB=9,点P是菱形ABCD内一点,PB=PD=3$\sqrt{3}$,则AP的长为3$\sqrt{3}$或6$\sqrt{3}$.分析 分成P在OA上和P在OC上两种情况进行讨论,根据△ABD是等边三角形,即可求得OA的长度,在直角△OBP中利用勾股定理求得OP的长,则AP即可求得.
解答  解:设AC和BE相交于点O.
解:设AC和BE相交于点O.
当P在OA上时,
∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=9,OB=OD=$\frac{1}{2}$BD=$\frac{9}{2}$.
则AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{9}^{2}-(\frac{9}{2})^{2}}$=$\frac{9\sqrt{3}}{2}$.
在直角△OBP中,OP=$\sqrt{P{B}^{2}-O{B}^{2}}$=$\sqrt{(3\sqrt{3})^{2}-(\frac{9}{2})^{2}}$=$\frac{3\sqrt{3}}{2}$.
则AP=OA-OP-$\frac{9\sqrt{3}}{2}-\frac{3\sqrt{3}}{2}$=3$\sqrt{3}$;
当P在OC上时,AP=OA+OP=$\frac{9\sqrt{3}}{2}+\frac{3\sqrt{3}}{2}$=6$\sqrt{3}$.
故答案是:3$\sqrt{3}$或6$\sqrt{3}$.
点评 本题考查了菱形的性质,注意到P在AC上,应分两种情况进行讨论是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列计算正确的是( )
| A. | |-2|=-2 | B. | (-3)2=-9 | C. | $\root{3}{27}$=3 | D. | (-8)-8=0 |
 如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.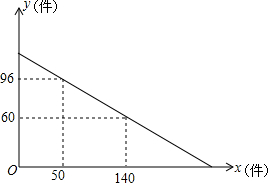 某服装店老板到批发中心批发A,B两种新款上衣,A种上衣的进货单价是B种上衣进货单价的1.5倍,考虑到各种因素,预计批发A种上衣数量y(件)与B种上衣的数量x(件)之间的函数关系如图所示,已知若批发的A,B 两种上衣中,A种有80件时,A,B两种上衣共需16800元.
某服装店老板到批发中心批发A,B两种新款上衣,A种上衣的进货单价是B种上衣进货单价的1.5倍,考虑到各种因素,预计批发A种上衣数量y(件)与B种上衣的数量x(件)之间的函数关系如图所示,已知若批发的A,B 两种上衣中,A种有80件时,A,B两种上衣共需16800元.  如图,直线y=-3x+3与x轴、y轴分别交于点A、B.抛物线y=a(x-2)2+k经过A、B,并与x轴交于另一点C,其顶点为P,
如图,直线y=-3x+3与x轴、y轴分别交于点A、B.抛物线y=a(x-2)2+k经过A、B,并与x轴交于另一点C,其顶点为P,