题目内容
11. 如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.(1)填空:∠AOC=50°,∠FOD=25度;
(2)∠AOC=α°.则∠EOD==(90-$\frac{1}{2}$α)°(用含α的式子表示);
(3)探究∠EOD与∠FOD的数量关系,并说明理由.
分析 (1)根据对顶角相等得到的度数,再根据OF平分∠BOD,即可解答;
(2)根据OE平分∠AOD,得到∠EOD=$\frac{1}{2}∠AOD$,根据∠AOD=180°-∠AOC=(180-α)°,即可解答;
(3)利用角平分线的性质和邻补角,计算出∠EOF的度数是90°,即可解答.
解答 解:(1)∵∠AOC=50°,
∴∠BOD=∠AOC=50°,
∵OF平分∠BOD,
∴∠FOD=$\frac{1}{2}∠BOD=2{5}^{°}$;
故答案为:25.
(2)∵OE平分∠AOD,
∴∠EOD=$\frac{1}{2}∠AOD$,
∵∠AOD=180°-∠AOC=(180-α)°,
∴∠EOD=$\frac{1}{2}$(180-α)°=(90-$\frac{1}{2}$α)°.
故答案为:=(90-$\frac{1}{2}$α)°.
(3)∠EOD+∠FOD=90°,
理由:∵OE平分∠AOD,OF平分∠BOD,
∴∠DOE=$\frac{1}{2}$∠AOD,∠DOF=$\frac{1}{2}$∠BOD,
∵∠BOD+∠AOD=180°,
∴∠DOE+∠DOF=$\frac{1}{2}$(∠BOD+∠AOD)=90°.
点评 本题考查角平分线的定义,邻补角,是基础题,熟记性质并准确识图,找出图中各角之间的关系是解题的关键.

练习册系列答案
相关题目
3.正方形具有而菱形不一定具有的特征有( )
| A. | 对角线互相垂直平分 | B. | 内角和为360° | ||
| C. | 对角线相等 | D. | 对角线平分内角 |
 如图,AB∥EF,DE∥BC,AB交DE于点O,请判断∠B与∠E的数量关系,并说明理由.
如图,AB∥EF,DE∥BC,AB交DE于点O,请判断∠B与∠E的数量关系,并说明理由.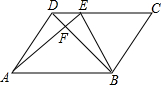 在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF=1:4:16.
在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF=1:4:16. 如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为$\frac{3\sqrt{5}}{5}$.
如图,正方形ABCD的边长为3,点0是对角线AC,BD的交点,点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足为F,连接OF,则OF的长为$\frac{3\sqrt{5}}{5}$.