题目内容
13.关于($\sqrt{a}$)2与$\sqrt{a^2}$,下列结论中正确的是( )| A. | a是任意实数时,都有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | B. | 只有a是正数时,才有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | ||
| C. | 当a为有理数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | D. | 当a≥0时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 |
分析 根据二次根式的性质进行判断即可.
解答 解:A、a是非负数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立,错误;
B、a是非负数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立,错误;
C、a是非负数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立,错误;
D、a是非负数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立,正确;
故选D.
点评 此题考查二次根式的性质,关键是根据a是非负数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立解答.

练习册系列答案
相关题目
4.在图形旋转中,下列说法错误的是( )
| A. | 图形上各点的旋转角度相同 | |
| B. | 对应点到旋转中心距离相等 | |
| C. | 旋转不改变图形的大小、形状 | |
| D. | 由旋转得到的图形也一定可以由平移得到 |

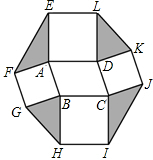 以?ABCD的四条边为边,在其形外分别作正方形,如图,连接EF、GH、IJ、KL.若?ABCD的面积为5,则图中阴影部分四个三角形的面积和为( )
以?ABCD的四条边为边,在其形外分别作正方形,如图,连接EF、GH、IJ、KL.若?ABCD的面积为5,则图中阴影部分四个三角形的面积和为( )
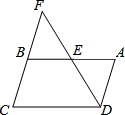 如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.
如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.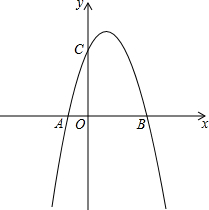 如图所示,抛物线y=ax2+bx+3与x轴交于点A、B两点(A在B的左侧)与y轴交于C点,且OA:OC=1:3,S△ABC=6.
如图所示,抛物线y=ax2+bx+3与x轴交于点A、B两点(A在B的左侧)与y轴交于C点,且OA:OC=1:3,S△ABC=6.