题目内容
7.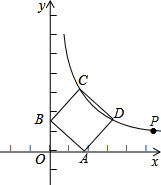 如图,点P($\sqrt{3}$+1,$\sqrt{3}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图,点P($\sqrt{3}$+1,$\sqrt{3}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y=$\frac{k}{x}$(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
分析 (1)将点P的坐标代入双曲线解析式中解答即可;
(2)过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,易证得△CFB≌△BOA≌△AED,易得C(b,a+b),D(a+b,a),继而求得a的值,则可求得点C的坐标;
解答 解:(1)点P($\sqrt{3}+1$,$\sqrt{3}-1$)在双曲线$y=\frac{k}{x}(x>0)$上,
将x=$\sqrt{3}+1$,y=$\sqrt{3}-1$代入解析式可得:
k=2;
(2)过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,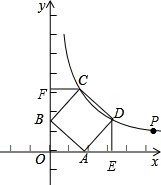
∵四边形ABCD是正方形,
∴AB=AD=BC,∠CBA=90°,
∴∠FBC+∠OBA=90°,
∵∠CFB=∠BOA=90°,
∴∠FCB+∠FBC=90°,
∴∠FBC=∠OAB,
在△CFB和△AOB中,
$\left\{\begin{array}{l}{∠CFB=∠AOB}\\{∠FBC=∠OAB}\\{CB=AB}\end{array}\right.$,
∴△CFB≌△AOB(AAS),
同理可得:△BOA≌△AED≌△CFB,
∴CF=OB=AE=b,BF=OA=DE=a,
设A(a,0),B(0,b),
则D(a+b,a)C(b,a+b),
可得:b(a+b)=2,a(a+b)=2,
解得:a=b=1.
所以点C的坐标为:(1,2).
点评 此题属于反比例函数的综合题,考查了待定系数法求函数的解析式、正方形的性质与判定、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,综合性很强,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
20.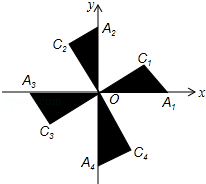 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | -3×($\frac{3\sqrt{3}}{2}$)2013 | C. | (2$\sqrt{3}$)2014 | D. | 3×($\frac{2\sqrt{3}}{3}$)2013 |
19.点P是直线l外一点,点A、B、C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为( )
| A. | 6 | B. | 8 | C. | 不大于6的数 | D. | 小于6的数 |
16.2015年是第23个“世界水日”,为鼓励居民节约用水,某市规定如下用水收费标准:每户每月的用水量不超过6m3时,水费按a元/立方米收费;超过时,不超过6m3的部分仍按a元/立方米收费,超过的部分按c元/立方米(c>a)收费,已知该市小明家今年3月份和4月份的用水量、水费如表所示:
(1)求a,c的值;
(2)设某户1个月的用水量为x(m3),应交水费y(元)
①分别写出用水量不超过6m3和超过6m3时,y与x之间的函数关系式;
②已知一户5月份的用水量为8m3,求该户5月份的水费.
| 月份 | 用水量/m3 | 水费/元 |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
(2)设某户1个月的用水量为x(m3),应交水费y(元)
①分别写出用水量不超过6m3和超过6m3时,y与x之间的函数关系式;
②已知一户5月份的用水量为8m3,求该户5月份的水费.
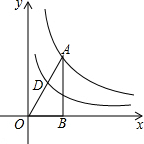 如图,反比例函数y=$\frac{2}{x}$的图象经过△ABO的顶点A,点D是OA的中点,若反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为$\frac{1}{2}$.
如图,反比例函数y=$\frac{2}{x}$的图象经过△ABO的顶点A,点D是OA的中点,若反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为$\frac{1}{2}$.