题目内容
3.一串数:$\frac{1}{1}$,-$\frac{1}{2}$,$\frac{2}{2}$,-$\frac{1}{2}$,$\frac{1}{3}$,-$\frac{2}{3}$,$\frac{3}{3}$,-$\frac{2}{3}$,$\frac{1}{3}$,-$\frac{1}{4}$,$\frac{2}{4}$,-$\frac{3}{4}$,$\frac{4}{4}$,-$\frac{3}{4}$,$\frac{2}{4}$,-$\frac{1}{4}$….(1)试问-$\frac{4}{5}$是第几个数?
(2)试问$\frac{7}{11}$是第几个数?
分析 分母是1的分数有1个,分母是2的分数由3个,分母是3的分数有5个,…分母是n的分数有2n-1个分数,先根据分母的变换规律,得出分母小于5的数的个数以及分母小于11的数的个数,再根据-$\frac{4}{5}$在分母为5的数中的位置,以及$\frac{7}{11}$在分母为11的数中的位置,分别判断它们在一串数中的位置即可.
解答 解:(1)分母为1的数有1×2-1=1个,
分母为2的数有2×2-1=3个,
分母为3的数有2×3-1=5个,
分母为4的数有2×4-1=7个,
故分母小于5的数有:1+3+5+7=16个,
∵分母为5的数有2×5-1=9个,其中的第4个和第6个为-$\frac{4}{5}$,
∴-$\frac{4}{5}$是第20个数和第22个数;
(2)由(1)得,分母为10的数有2×10-1=19个,
故分母小于11的数有:1+3+5+…+19=$\frac{(1+19)10}{2}$=100个,
∵分母为11的数有2×11-1=21个,其中的第7个和第15个为$\frac{7}{11}$,
∴$\frac{7}{11}$是第107个数和第115个数.
点评 本题主要考查了数字变化规律类问题,认真观察、仔细思考,善用联想是解决这类问题的方法.解题时注意:分子都是从1开始到与分母的数字相同连续的自然数,再递减到1,此规律是解决问题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
13.在平面直角坐标系中,点P(-2,a)与点Q(b,3)关于原点对称,则a+b的值为( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
11.若方程组$\left\{\begin{array}{l}{5x+6y-8z=12}\\{x+4y-z=-1}\\{2x+3y-4z=5}\end{array}\right.$的解为(a,b,c),则a+b+c=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
15.三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长是( )
| A. | 9 | B. | 11 | C. | 13 | D. | 11或13 |
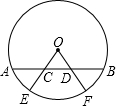 已知:如图,AB是⊙O的弦,且AC=BD,半径OE,OF分别过C,D两点,求证:$\widehat{AE}$=$\widehat{BF}$.
已知:如图,AB是⊙O的弦,且AC=BD,半径OE,OF分别过C,D两点,求证:$\widehat{AE}$=$\widehat{BF}$.