��Ŀ����
4��һ�죬С������ֽƬƴͼ��Ϸʱ����������ͼ���е����ֲ��ϸ����ɣ�����ƴ��һЩ������������ijЩ��ʽ������ͼ�ڿ��Խ���Ϊ��ʽ����a+2b����a+b��=a2+3ab+2b2����1����ͼ�ۿ��Խ���Ϊ��ʽ����2a+b����a+2b��=2a2+5ab+2b2��
��2�������߿�����ͼ���еĻ���ͼ�����ɿ飨ÿ��������һ�Σ�ƴ��һ�������Σ�ʹƴ���ij��������Ϊa2+4ab+3b2��������ͼ�б����������εij��Ϳ���
��3����ͼ�ܣ��������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ������ε����߳���x��y�����۲�ͼ����ָ�����¹�ϵʽ����a��x-y=n����b��xy=$\frac{{m}^{2}-{n}^{2}}{4}$����c��x2-y2=mn����d��x2+y2=$\frac{{m}^{2}+{n}^{2}}{2}$��������ȷ�Ĺ�ϵʽ�ĸ�����4����
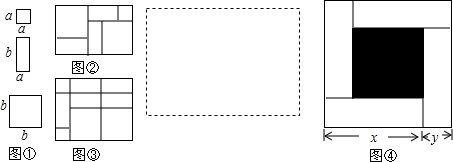
���� ��1����ͼ���ɵó������ʽ�ӣ�
��2�������ľ��α߳��ֱ�Ϊ��a+b���ͣ�a+3b�����ɣ�
��3������ͼ��ÿ��ͼ�ε����֮��Ĺ�ϵ�����жϳ���ȷ���м�����
��� �⣺��1���ɷ���֪��ͼ������ʾ�ĵ�ʽΪ����2a+b����a+2b��=2a2+5ab+2b2��
�ʴ�Ϊ����2a+b����a+2b��=2a2+5ab+2b2��
��2��ʾ��ͼ���£�
��3����a����ȷ����b����4xy=m2-n2����xy=$\frac{{m}^{2}-{n}^{2}}{4}$����ȷ��
��c����x+y=m��x-y=n��
��x2-y2=��x+y����x-y��=mn��
����ȷ��
��d��${x}^{2}+{y}^{2}=��x-y��^{2}+2xy={n}^{2}-2��\frac{{m}^{2}-{n}^{2}}{4}$=$\frac{{m}^{2}+{n}^{2}}{2}$����ȷ��
����ȷ����4�����ʴ�Ϊ��4��
���� ���⿼������ȫƽ����ʽ����ʽ�Ļ�������Ӧ�ã���Ҫ����ѧ���ļ��������۲�ͼ�ε�������

��ϰ��ϵ�д�
 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
�����Ŀ
12����Rt��ABC�У���C=90�㣬��sinA=$\frac{2}{3}$����tanB=��������
| A�� | $\frac{5}{3}$ | B�� | $\frac{\sqrt{5}}{3}$ | C�� | $\frac{2\sqrt{5}}{5}$ | D�� | $\frac{\sqrt{5}}{2}$ |
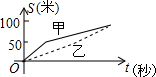
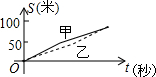
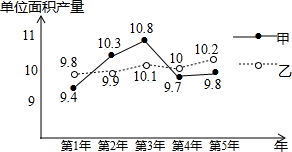 �ס�������ˮ��Ʒ�־�������5��������ֲ��ÿ��ĵ�λ�������������ͼ��ͼ��ʾ���������㣬�ĵ�λ���ƽ������$\overline{x}$��=10���ҵĵ�λ���ƽ������$\overline{x}$��=10�������ͼ�����ƣ�����ˮ��Ʒ�ֲ����Ƚ��ȶ������ң�
�ס�������ˮ��Ʒ�־�������5��������ֲ��ÿ��ĵ�λ�������������ͼ��ͼ��ʾ���������㣬�ĵ�λ���ƽ������$\overline{x}$��=10���ҵĵ�λ���ƽ������$\overline{x}$��=10�������ͼ�����ƣ�����ˮ��Ʒ�ֲ����Ƚ��ȶ������ң�
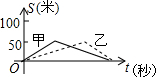
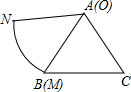 ��ͼ������OMN����������ABC���뾶OM��AB�غϣ����λ�MN�ij�ΪAB�ij�����֪AB=10�����������������η������״�����ʼλ����ͬ�����O������·����10+$\frac{70��}{3}$��
��ͼ������OMN����������ABC���뾶OM��AB�غϣ����λ�MN�ij�ΪAB�ij�����֪AB=10�����������������η������״�����ʼλ����ͬ�����O������·����10+$\frac{70��}{3}$��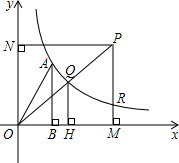 ��ͼ������y=$\frac{k}{x}$��x��0��������A��1��2��������A��AB��x���ڵ�B������OA����PΪ��һ�����������Ϸ�һ���㣬����P�ֱ���PM��x���ڵ�M��PN��y���ڵ�N��PM�������ڵ�R������PO�������ڵ�Q������Q��QH��x���ڵ�H��
��ͼ������y=$\frac{k}{x}$��x��0��������A��1��2��������A��AB��x���ڵ�B������OA����PΪ��һ�����������Ϸ�һ���㣬����P�ֱ���PM��x���ڵ�M��PN��y���ڵ�N��PM�������ڵ�R������PO�������ڵ�Q������Q��QH��x���ڵ�H��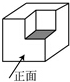 ��ͼ�ļ���������һ����������ȥһ��С�������γɵģ���������ͼ�ǣ�������
��ͼ�ļ���������һ����������ȥһ��С�������γɵģ���������ͼ�ǣ�������



