题目内容
5.对于任意的实数p,q,定义运算“*”:$p*q=\frac{q}{p+q}$(p≠-q).已知a1=x,a2=1*a1,a3=1*a2,a4=1*a3,…,依此类推,可以得到一列数a1,a2,a3,a4,….当x=2时,a3=$\frac{2}{5}$,a2014=$\frac{2}{4027}$;经小丁探究发现,当x取某些特定的值,例如当x=-1时,无法计算出a4的值,这样的x的取值还可能为$-\frac{1}{2}和-\frac{1}{3}$.(请写出所有满足条件的值)分析 (1)当x=2时,a1=2,a2=1*2=$\frac{2}{1+2}=\frac{2}{3}$,a3=1*$\frac{2}{3}$=$\frac{\frac{2}{3}}{1+\frac{2}{3}}=\frac{2}{5}$,a4=1*$\frac{2}{5}$=$\frac{\frac{2}{5}}{1+\frac{2}{5}}=\frac{2}{7}$,…,所以这列数a1,a2,a3,a4,…,每一个数的分子都是2,an的分母是2n-1,据此求出a2014的值是多少即可;
(2)根据题意,无法计算出a4的值,则a2=-1或a3=-1,分别令a2=-1,a3=-1,求出这样的x的取值还可能为多少即可.
解答 解:(1)当x=2时,a1=2,
a2=1*2=$\frac{2}{1+2}=\frac{2}{3}$,
a3=1*$\frac{2}{3}$=$\frac{\frac{2}{3}}{1+\frac{2}{3}}=\frac{2}{5}$,
a4=1*$\frac{2}{5}$=$\frac{\frac{2}{5}}{1+\frac{2}{5}}=\frac{2}{7}$,
…,
所以这列数a1,a2,a3,a4,…,每一个数的分子都是2,an的分母是2n-1,
所以a2014=$\frac{2}{2×2014-1}=\frac{2}{4027}$;
(2)令a2=-1,
则$\frac{x}{1+x}=-1$,
解得x=-$\frac{1}{2}$;
令a3=-1,
则$\frac{{a}_{2}}{1{+a}_{2}}=-1$,
解得${a}_{2}=-\frac{1}{2}$,
所以$\frac{x}{1+x}$=-$\frac{1}{2}$,
解得x=-$\frac{1}{3}$,
综上,可得这样的x的取值还可能为$-\frac{1}{2}和-\frac{1}{3}$.
故答案为:$\frac{2}{5};\frac{2}{4027}$;$-\frac{1}{2}和-\frac{1}{3}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:这列数a1,a2,a3,a4,…,每一个数的分子都是2,an的分母是2n-1.

 智能训练练测考系列答案
智能训练练测考系列答案 如图,小张与小王分别从相距300公里的甲、乙两地同时出发,相向而行.小张骑摩托车到达乙地后立即返回甲地,小王从乙地直接到达甲地.y1表示小张离甲地的距离,y2表示小王离乙地的距离.则两人从出发到第一次相遇用时( )
如图,小张与小王分别从相距300公里的甲、乙两地同时出发,相向而行.小张骑摩托车到达乙地后立即返回甲地,小王从乙地直接到达甲地.y1表示小张离甲地的距离,y2表示小王离乙地的距离.则两人从出发到第一次相遇用时( )| A. | $\frac{24}{13}$时 | B. | $\frac{24}{11}$时 | C. | $\frac{64}{13}$时 | D. | $\frac{64}{11}$时 |
| A. | $\frac{180}{x}$-$\frac{180}{x+2}$=3 | B. | $\frac{180}{x+2}$-3180x=3 | C. | $\frac{180}{x}$-$\frac{180}{x-2}$=3 | D. | $\frac{180}{x-2}$-$\frac{180}{x}$=3 |
 D.
D. 

 的结果是( )
的结果是( )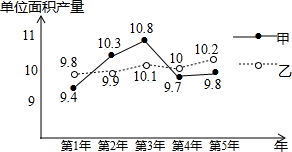 甲、乙两种水稻品种经过连续5年试验种植,每年的单位面积产量的折线图如图所示,经过计算,甲的单位面积平均产量$\overline{x}$甲=10,乙的单位面积平均产量$\overline{x}$乙=10,则根据图表估计,两种水稻品种产量比较稳定的是乙.
甲、乙两种水稻品种经过连续5年试验种植,每年的单位面积产量的折线图如图所示,经过计算,甲的单位面积平均产量$\overline{x}$甲=10,乙的单位面积平均产量$\overline{x}$乙=10,则根据图表估计,两种水稻品种产量比较稳定的是乙.