题目内容
 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.(1)画出△A1OB1并写出点B1的坐标为
(2)写出△A1OB1的面积为
(3)点P在x轴上,使PA+PB的值最小,写出点P的坐标为
考点:作图-轴对称变换,轴对称-最短路线问题
专题:作图题
分析:(1)根据网格结构找出点A、B关于y轴的对称点A1、B1的位置,再与O顺次连接即可,然后根据平面直角坐标系写出点B1的坐标;
(2)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解;
(3)找出点A关于x轴的对称点A′位置,连接A′B,根据轴对称确定最短路线问题与x轴的交点即为所求的点P.
(2)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解;
(3)找出点A关于x轴的对称点A′位置,连接A′B,根据轴对称确定最短路线问题与x轴的交点即为所求的点P.
解答: 解:(1)△A1OB1如图所示,B1(-1,3);
解:(1)△A1OB1如图所示,B1(-1,3);
(2)△A1OB1的面积=3×3-
×1×2-
×2×3-
×1×3
=9-1-3-1.5
=9-5.5
=3.5;
(3)如图所示,点P的坐标为(2.2,0).
故答案为:(1)(-1,3);(2)3.5;(3)(2.2,0).
 解:(1)△A1OB1如图所示,B1(-1,3);
解:(1)△A1OB1如图所示,B1(-1,3);(2)△A1OB1的面积=3×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=9-1-3-1.5
=9-5.5
=3.5;
(3)如图所示,点P的坐标为(2.2,0).
故答案为:(1)(-1,3);(2)3.5;(3)(2.2,0).
点评:本题考查了利用轴对称变换作图,三角形的面积,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
 已知:如图,BD平分∠ABC,∠ABD=3∠DBE,∠ABE=40°,求∠EBC的度数.
已知:如图,BD平分∠ABC,∠ABD=3∠DBE,∠ABE=40°,求∠EBC的度数.
 在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.
在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.
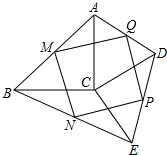 如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形.
如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形. 如图,给下列条件:
如图,给下列条件: