题目内容
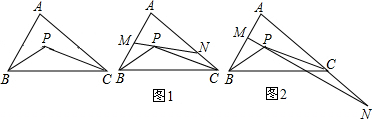
如图,已知△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)若∠ABC=80°,∠ACB=50°,则∠BPC= 度;
(2)若∠A=x°,试求∠BPC的度数(用含x的代数式表示);
(3)现将一直线MN绕点P旋转.
①当直线MN与AB、AC的交点M、N分别在线段AB和AC上时(如图1),试求∠MPB、∠NPC、∠A三者之间的数量关系,并说明理由;
②当直线MN与AB的交点M在线段AB上,与AC的交点N在AC的延长线上时(如图2),试问①中的数量关系是否仍然成立?若成立,请说明理由;若不成立,请写出正确的数量关系,并说明理由.
(1)若∠ABC=80°,∠ACB=50°,则∠BPC=
(2)若∠A=x°,试求∠BPC的度数(用含x的代数式表示);
(3)现将一直线MN绕点P旋转.
①当直线MN与AB、AC的交点M、N分别在线段AB和AC上时(如图1),试求∠MPB、∠NPC、∠A三者之间的数量关系,并说明理由;
②当直线MN与AB的交点M在线段AB上,与AC的交点N在AC的延长线上时(如图2),试问①中的数量关系是否仍然成立?若成立,请说明理由;若不成立,请写出正确的数量关系,并说明理由.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)求出∠PBC=40°,∠PCB=25°,再根据三角形内角和定理推出即可;
(2)求出∠ABC+∠ACB,求出∠PBC+∠PCB,再根据三角形内角和定理求出即可;
(3)①根据∠MPB+∠NPC=180°-∠BPC和∠BPC=90°+
∠A,代入求出即可;②根据∠MPB=180°-(∠BPC-∠NCP)和∠BPC=90°+
∠A,代入求出即可.
(2)求出∠ABC+∠ACB,求出∠PBC+∠PCB,再根据三角形内角和定理求出即可;
(3)①根据∠MPB+∠NPC=180°-∠BPC和∠BPC=90°+
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵∠ABC与∠ACB的平分线相交于点P,
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∵∠ABC=80°,∠ACB=50°,
∴∠PBC=40°,∠PCB=25°,
∴∠BPC=180°-∠PBC-∠PCB=115°,
故答案为:115;
(2)∵∠ABC与∠ACB的平分线相交于点P
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-(
∠ABC+
∠ACB)
=180°-
(180°-∠A)
=90°+
∠A
=90°+
x°;
(3)①∠MPB+∠NPC=90°-
∠A,
理由如下:
∵∠BPC=90°+
∠A,
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A)
=90°-
∠A;
②原结论不成立,正确的是∠MPB-∠NPC=90°-
∠A,
理由如下:
由图可知∠MPB+∠BPC-∠NPC=180°,
由知①:∠BPC=90°+
∠A,
∴∠MPB-∠NPC=180°-∠BPC
=180°-(90°+
∠A)
=90°-
∠A.
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=80°,∠ACB=50°,
∴∠PBC=40°,∠PCB=25°,
∴∠BPC=180°-∠PBC-∠PCB=115°,
故答案为:115;
(2)∵∠ABC与∠ACB的平分线相交于点P
∴∠BPC=180°-(∠PBC+∠PCB)
=180°-(
| 1 |
| 2 |
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
(3)①∠MPB+∠NPC=90°-
| 1 |
| 2 |
理由如下:
∵∠BPC=90°+
| 1 |
| 2 |
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
②原结论不成立,正确的是∠MPB-∠NPC=90°-
| 1 |
| 2 |
理由如下:
由图可知∠MPB+∠BPC-∠NPC=180°,
由知①:∠BPC=90°+
| 1 |
| 2 |
∴∠MPB-∠NPC=180°-∠BPC
=180°-(90°+
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
点评:本题考查了角平分线定义,三角形的内角和定理的应用,主要考查学生的推理能力,题目综合性比较强,有一定的难度.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
小亮解方程组
的解为
,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和◆,则这两个数●和◆的值为( )
|
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(-1,2),点B坐标为(-2,0).
如图,在平面直角坐标系中,点O是坐标原点,点A的坐标为(-1,2),点B坐标为(-2,0). 已知:如图,BD平分∠ABC,∠ABD=3∠DBE,∠ABE=40°,求∠EBC的度数.
已知:如图,BD平分∠ABC,∠ABD=3∠DBE,∠ABE=40°,求∠EBC的度数.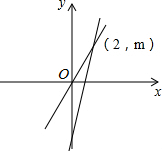 如图,已知一次函数y=kx+b经过(-1,-5)且与正比例函数y=2x的图象相交于(2,m)点.
如图,已知一次函数y=kx+b经过(-1,-5)且与正比例函数y=2x的图象相交于(2,m)点.
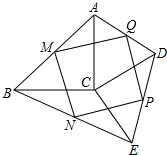 如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形.
如图,在△ABC和△DCE中,BC=AC,DC=CE,∠ACB=∠DCE=90°,且AB,BD,DE,EA的中点分别是点M,N,P,Q.求证:四边形MNPQ是菱形.