题目内容
17.已知函数y=y1+y2,其中y1与x+1成反比例,y2与x2成正比例,当x=1时,y=2,当x=0时,y=2.(1)求y与x的函数关系式;
(2)求x的取值范围;
(3)当x=-5和x=3时,函数y的值是多少?
分析 (1)根据反比例函数与正比例函数定义可设y1=$\frac{a}{x+1}$,y2=bx2,则y=$\frac{a}{x+1}$+bx2,再把两组对应值分别代入得到a和b的方程组,解方程组求出a和b即可得到y与x的函数关系式;
(2)利用分母不为零即可得到x的取值范围;
(3)把x=-5和x=3分别代入(1)中的函数关系式中可计算对应的y的值.
解答 解:(1)设y1=$\frac{a}{x+1}$,y2=bx2,则y=$\frac{a}{x+1}$+bx2,
把x=1,y=2;x=0,y=2分别代入得$\left\{\begin{array}{l}{\frac{a}{2}+b=2}\\{a=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
所以y与x的函数关系式为y=$\frac{2}{x+1}$+x2;
(2)x+1≠0,即x≠-1;
(3)当x=-5时,y=$\frac{2}{x+1}$+x2=$\frac{2}{-5+1}$+(-5)2=24.5;
当x=3,y=$\frac{2}{x+1}$+x2=$\frac{2}{3+1}$+32=9.5.
点评 本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
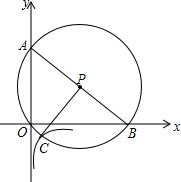 如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.
如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.