题目内容
13．已知实数a，b满足|2017-a|+$\sqrt{a-2018}$=a，则代数式a-20172=（ ）| A． | 2016 | B． | 2017 | C． | 2018 | D． | 2019 |
分析 根据二次根式有意义的条件以及绝对值的性质即可求出答案．
解答 解：由二次根式有意义的条件可知：a-2018≥0，
∴a≥2018，
∴2017-a＜0，
∵|2017-a|+$\sqrt{a-2018}$=a，
∴a-2017+$\sqrt{a-2018}$=a，
∴a=2018+20172，
∴a-20172=2018，
故选（C）
点评 本题考查二次根式有意义的条件，解题的关键是正确理解二次根式有意义的条件，本题属于基础题型．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
17．下列所述图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． | 等边三角形 | B． | 平行四边形 | C． | 正五边形 | D． | 圆 |
4．10名学生的身高如下（单位：cm）159、169、163、170、166、165、156、172、165、162，从中任选一名学生，其身高超过165cm的概率是（ ）
| A． | 0.5 | B． | 0.4 | C． | 0.2 | D． | 0.1 |
1．在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，某学习小组做了摸球实验，他们将30个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是几次活动汇总后统计的数据：
（1）请估计：当次数s很大时，摸到白球的频率将会接近0.3；假如你去摸一次，你摸到白球的概率是0.7（精确到0.1）．
（2）试估算口袋中红球有多少只？
（3）解决了上面的问题后请你从统计与概率方面谈一条启示．
| 摸球的次数s | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率$\frac{n}{s}$ | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
（2）试估算口袋中红球有多少只？
（3）解决了上面的问题后请你从统计与概率方面谈一条启示．
18．
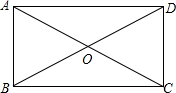如图，下列条件中，能使?ABCD成为矩形是（ ）
如图，下列条件中，能使?ABCD成为矩形是（ ）| A． | AB=AD | B． | ∠ABO=60° | C． | AO=BO | D． | AC⊥BD |
5．下列各数中，绝对值最大的数是（ ）
| A． | 5 | B． | -3 | C． | 0 | D． | -6 |
2．如果一个角的补角是120°，那么这个角的度数是（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 120° |
