题目内容
11.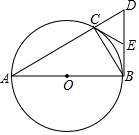 如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.(1)E为BD的中点,连结CE,求证:CE是⊙O的切线;
(2)若AC=3CD,求∠A的大小.
分析 (1)连接OC,根据等腰三角形的性质得到∠A=∠1,根据三角形的中位线的性质得到OE∥AD,得到∠2=∠3,根据全等三角形的性质得到∠OCE=∠ABD=90°,于是得到CE是⊙O的切线;
(2)由AB为⊙O的直径,得到BC⊥AD,根据相似三角形的性质得到BC2=AC•CD,得到tan∠A=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$,于是得到结论.
解答 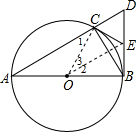 解:(1)连接OC,
解:(1)连接OC,
∵OA=OC,
∴∠A=∠1,
∵AO=OB,E为BD的中点,
∴OE∥AD,
∴∠1=∠3,∠A=∠2,
∴∠2=∠3,
在△COE与△BOE中,$\left\{\begin{array}{l}{OC=OB}\\{∠2=∠3}\\{OE=OE}\end{array}\right.$,
∴△COE≌△BOE,
∴∠OCE=∠ABD=90°,
∴CE是⊙O的切线;
(2)∵AB为⊙O的直径,
∴BC⊥AD,
∵AB⊥BD,
∴△ABC∽△BDC,
∴$\frac{BC}{AC}=\frac{CD}{BC}$,
∴BC2=AC•CD,
∵AC=3CD,
∴BC2=$\frac{1}{3}$AC2,
∴tan∠A=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°.
点评 本题考查了切线的判定和性质,相似三角形的判定和性质,全等三角形的判定和性质,三角形中位线的性质,三角函数的定义,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
1.在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
(1)请估计:当次数s很大时,摸到白球的频率将会接近0.3;假如你去摸一次,你摸到白球的概率是0.7(精确到0.1).
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
| 摸球的次数s | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率$\frac{n}{s}$ | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
2.如果一个角的补角是120°,那么这个角的度数是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
19.要使式子$\frac{{\sqrt{x+2}}}{x-1}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≤-2 | C. | x≥1 | D. | x≥-2 且x≠1 |
6.中国超级计算机神威“太湖之光”,峰值计算速度达每秒12.5亿亿次,为世界首台每秒超10亿亿次运算的计算机,用科学记数法表示12.5亿亿次/秒为( )亿次/秒.
| A. | 12.5×108 | B. | 12.5×109 | C. | 1.25×108 | D. | 1.25×109 |
20.如果2是方程x2-3x+k=0的一个根,则常数k的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
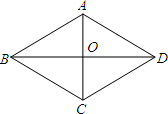 求证:对角线互相垂直的平行四边形是菱形.
求证:对角线互相垂直的平行四边形是菱形.