题目内容
13. 在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
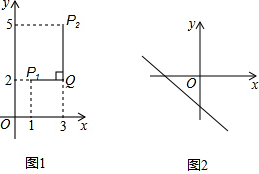
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点A(0,1),B为y轴上的一个动点,若点A与点B的“非常距离”为3,写出满足条件的点B的坐标(0,4)或(0,-2).
分析 根据意义可知点A、B均在y轴上,故此|yB-1|=3,从而可求得点B的纵坐标,故此可求得点B的坐标.
解答 解:∵点A的坐标为(0,1),
∴点A在y轴上.
∵点B也在y轴上,且点A与点B的“非常距离”为3,
∴|yB-1|=3.
解得:yB=4或yB=-2.
∴点B的坐标为(0,4)或(0,-2).
故答案为:(0,4)或(0,-2).
点评 本题主要考查的是坐标与图形的性质、新定义,根据定义得出|yB-1|=3是解题的关键.

练习册系列答案
相关题目
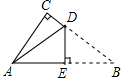 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,求BD的长度.
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,求BD的长度.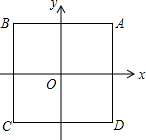 如图,在坐标系中,点O是边长为2的正方形ABCD的中心,函数y=x2+c,使它的图象与正方形ABCD有公共点,则c的取值范围是-2≤c≤1.
如图,在坐标系中,点O是边长为2的正方形ABCD的中心,函数y=x2+c,使它的图象与正方形ABCD有公共点,则c的取值范围是-2≤c≤1.