题目内容
11.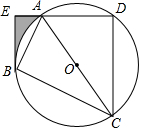 如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.(1)判断BE与⊙O的位置关系,并说明理由;
(2)若∠ACB=30°,⊙O的半径为2,请求出图中阴影部分的面积.
分析 (1)连接BO,根据等腰三角形的性质得到∠1=∠2,根据角平分线的定义得到∠1=∠BAE,等量代换得到∠2=∠BAE,根据余角的性质得到∠EBO=90°,于是得到结论;
(2)根据已知条件得到△ABO是等边三角形,得到∠2=60°,解直角三角形得到BE=$\sqrt{3}$,于是得到结论.
解答 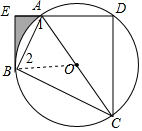 解:(1)BE与⊙O相切,
解:(1)BE与⊙O相切,
理由:连接BO,∵OA=OB,
∴∠1=∠2,
∵AB平分∠CAE,
∴∠1=∠BAE,
∴∠2=∠BAE,
∵BE⊥AD,
∴∠AEB=90°,
∴∠ABE+∠BAE=90°,
∴∠ABE+∠2=90°,即∠EBO=90°,
∴BE⊥OB,
∴BE与⊙O相切;
(2)∵∠ACB=30°,
∴∠AOB=60°,
∵OA=OB,
∴△ABO是等边三角形,
∴∠2=60°,OA=OB=AB=2,
∴∠ABE=30°,
在Rt△ABE中,cos∠ABE=$\frac{BE}{AB}=\frac{\sqrt{3}}{2}$,
∴BE=$\sqrt{3}$,
∴AE=1,
∴S阴影=S四边形AEBO-S扇形AOB=$\frac{3\sqrt{3}}{2}-\frac{2}{3}π$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形的计算.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
19.下列事件中,属于不可能事件的是( )
| A. | 射击运动员射击一次,命中9环 | |
| B. | 今天是星期六,明天就是星期一 | |
| C. | 某种彩票中奖率为10%,买十张有一张中奖 | |
| D. | 在只装有10个红球的布袋中摸出一球,这个球一定是红球 |
10.有x支球队参加篮球比赛,共比赛了21场,每两队之间都比赛一场,则下列方程中符合题意的是( )
| A. | x(x-1)=21 | B. | x(x+1)=21 | C. | x(x-1)=42 | D. | x(x+1)=42 |
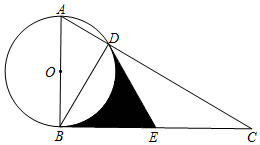 如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB
如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB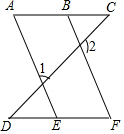 如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说:
如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说: