题目内容
2.解方程组:(1)$\left\{\begin{array}{l}{\frac{2(x-y)}{3}-\frac{x+y}{4}=-1}\\{3(x+y)-2(x-y)=6}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x-y+2z=-1}\\{4x+y+z=5}\\{x-2y-z=-2}\end{array}\right.$.
分析 (1)把x+y和x-y看做一个整体,再解答即可;
(2)先消去z后,再解二元一次方程组即可.
解答 解:(1)设x+y=a,x-y=b,原方程可化为:$\left\{\begin{array}{l}{\frac{2b}{3}-\frac{a}{4}=-1①}\\{3a-2b=6②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=-1}\end{array}\right.$,
即:$\left\{\begin{array}{l}{x+y=\frac{4}{3}}\\{x-y=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{1}{6}}\\{y=\frac{7}{6}}\end{array}\right.$,
(2)$\left\{\begin{array}{l}{3x-y+2z=-1①}\\{4x+y+z=5②}\\{x-2y-z=-2③}\end{array}\right.$,
②+③得:5x-y=3④,
①+②×2得:5x-5y=-5⑤,
把④代入⑤得:x=1,
把x=1代入④得:y=2,
把x=1,y=2代入①得:z=-1,
所以方程组的解是:$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=-1}\end{array}\right.$.
点评 本题考查了解三元一次方程组,解题的关键是掌握消元思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知$\frac{1}{a}$-$\frac{1}{b}$=$\frac{1}{3}$,则$\frac{ab}{6a-6b}$的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
12.某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶6元的价格出售,如果当天卖不完,剩余的只有倒掉.店主记录了30天的日需求量(单位:瓶),整理得下表:
(1)求这30天内日需求量的众数;
(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数;
(3)以30记录的各需求量的频率作为各需求是发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.
| 日需求量 | 26 | 27 | 28 | 29 | 30 |
| 频数 | 5 | 8 | 7 | 6 | 4 |
(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数;
(3)以30记录的各需求量的频率作为各需求是发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.
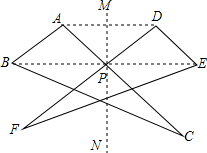 如图,三角形ABC沿着直线MN折叠后,与三角形DEF完全重合.
如图,三角形ABC沿着直线MN折叠后,与三角形DEF完全重合.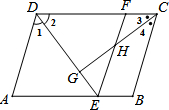 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可). 如图,在梯形ABCD中,AD∥BC,AD=3,AB=CD=4,∠A=120°,则下底BC的长为
如图,在梯形ABCD中,AD∥BC,AD=3,AB=CD=4,∠A=120°,则下底BC的长为 .
.