题目内容
12．如果△ABC的两边长分别为3和5，那么连结△ABC三边中点D、E、F所得的△DEF的周长可能是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 本题依据三角形三边关系，可求第三边大于2小于7，原三角形的周长大于10小于15，连接中点的三角形周长是原三角形周长的一半，那么新三角形的周长应大于5而小于7.5，看哪个符合就可以了．
解答 解：设三角形的三边分别是a、b、c，令a=3，b=5，
则2＜c＜7，10＜三角形的周长＜15，
故5＜中点三角形周长＜7.5．
故选D．
点评 本题考查了三角形的中位线定理，利用三角形三边关系，确定原三角形的周长范围是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
如图，C、D是线段AB上两点，已知图中所有线段的长度都是正整数，且总和为29，则线段AB的长度是（ ）
如图，C、D是线段AB上两点，已知图中所有线段的长度都是正整数，且总和为29，则线段AB的长度是（ ）| A． | 8 | B． | 9 | C． | 8或9 | D． | 无法确定 |
如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，cosC=$\frac{\sqrt{2}}{2}$，sinB=$\frac{1}{3}$，AD=1．
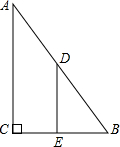有一直角三角形的硬纸板，∠C=90°，BC=2，∠B=60°，沿中位线DE剪成两部分，将这两部分再拼成一个四边形，这个四边形的周长为3+3$\sqrt{3}$．