题目内容
15.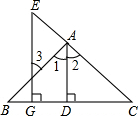 如图,已知AD⊥BC于D,EG⊥BC于G,AD平分∠BAC,
如图,已知AD⊥BC于D,EG⊥BC于G,AD平分∠BAC,求证:∠E=∠3.
分析 根据同位角相等两直线平行可得AD∥EG,根据平行线的性质可得∠1=∠3,∠E=∠3,利用角平分线的得出∠1=∠3,再利用等量代换可得∠E=∠3,
解答 证明:∵AD⊥BC于D,EG⊥BC于G,
∴∠ADC=∠EGC=90°,
∴AD∥EG,
∴∠1=∠3,∠E=∠3,
又∵AD平分∠BAC
∴∠1=∠3,
∴∠E=∠3
点评 本题考查的是平行线的判定与性质,用到的知识点为:同位角相等,两直线平行;两直线平行,内错角相等,同位角相等.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.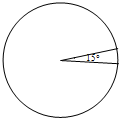 如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )
如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )
 如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )
如图,用不同颜色的马赛克覆盖一个圆形的台面,估计15°的圆心角的扇形部分大约需要34片马赛克片.已知每箱装有125片马赛克片,那么应该购买多少箱马赛克片才能铺满整个台面( )| A. | 5-6箱 | B. | 6-7箱 | C. | 7-8箱 | D. | 8-9箱 |
20.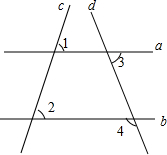 直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )
 直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )| A. | 70° | B. | 80° | C. | 100° | D. | 110° |
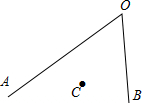 某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹) 如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:AF=DA.
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:AF=DA.