题目内容
17．
如图，⊙O的内接正三角形ABC的边心距OD为2cm，则⊙O的半径为4cm．
分析 连接OB，OC，求出∠BOC=120°，由等腰三角形的性质和三角形内角和定理得出∠OBC=30°，由直角三角形的性质得出OB=2OD即可．
解答 解：
连接OB、OC，如图所示：
则∠BOC=$\frac{360°}{3}$=120°，
∵OB=OC，
∴∠OBC=30°，
∵OD⊥BC，
∴OB=2OD=4cm；
故答案为：4．
点评 本题考查了等边三角形的性质、等腰三角形的性质、直角三角形的性质、三角形的外接圆半径；熟练掌握等边三角形的性质是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
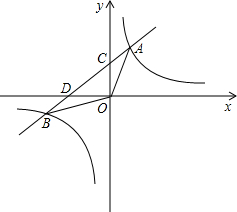如图，一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象相交于A、B两点，与y轴交于点C，与x轴交于点D，点D的坐标为（-3，0），A点的横坐标是3，tan∠CDO=$\frac{1}{3}$．
8．据统计结果显示，阳信县今年约有4500名学生参加中考，4500这个科学记数法可表示为（ ）
| A． | 4.5×102 | B． | 4.5×103 | C． | 4.5×104 | D． | 0.45×105 |
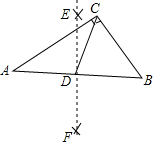如图，在△ABC中，∠ACB=90°，按一下步骤作图：分别以点A和点B为圆心，大于$\frac{1}{2}$AB的长为半径作圆弧，两弧交于点E和点F，作直线EF交AB于点D，连结CD，若AC=8，BC=6，则CD的长为5．
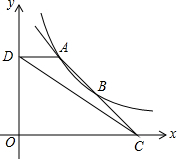如图，直线y=mx+n与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于A、B两点，交x轴于点C（$\frac{9}{2}$，0），过点A作AD⊥y轴于点D（0，$\frac{8}{3}$），连接CD，S△ADC=2．