题目内容
18．已知关于x的方程（2+k）x2+6kx+4k+1=0．（1）如果方程只有一个根，求k的值，并求此时方程的根；
（2）如果方程有两个相等的实根，求k的值，并求此时方程的根．
分析 （1）由题意得2+k=0，即k=-2，列出方程求解可得；
（2）根据题意得：2+k≠0且△=0，解方程可得m的值，再代入列出关于x的方程，求解可得．
解答 解：（1）根据题意得：2+k=0，即k=-2，
方程为-12x-7=0，
解得：x=-$\frac{7}{12}$；
（2）根据题意，得：2+k≠0，即k≠-2，△=0，即（6k）2-4（2+k）×（4k+1）=0，
解得：k=2或k=-$\frac{1}{5}$，
当k=2时，方程为4x2+12x+9=0，解得：x=-$\frac{3}{2}$，
当k=-$\frac{1}{5}$时，方程为$\frac{9}{5}$x2-$\frac{6}{5}$x+$\frac{1}{5}$=0，解得：x=$\frac{1}{3}$．
点评 本题主要考查根的判别式与一元二次方程的定义，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：①当△＞0时，方程有两个不相等的两个实数根；②当△=0时，方程有两个相等的两个实数根；③当△＜0时，方程无实数根．
练习册系列答案
相关题目
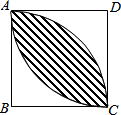如图所示，若正方形边长为a，则阴影部分的面积为（$\frac{1}{2}$π-1）a2．