题目内容
3.求所有的质数p,使4p2+1和6p2+1都是质数.分析 分p=5k、5k+1、5k+2、5k+3、5k+4(k为正整数)讨论,根据p、4p2+1和6p2+1都是质数找出符合题意p的值,综上即可得出结论.
解答 解:分p=5k、5k+1、5k+2、5k+3、5k+4(k为正整数)讨论.
当p=5k时,只有k=1,p=5时,为质数,
此时4p2+1=4×25+1=101为质数,6p2+1=6×25+1=151也为质数;
当p=5k+1时,4p2+1=4×(5k+1)2+1=100k2+40k+5=5(20k2+8k+1)能被5整除,
∴p=5k+1不合适;
当p=5k+2时,6p2+1=6×(5k+2)2+1=150k2+120k+25=5(30k2+24k+5)能被5整除,
∴p=5k+2不合适;
当p=5k+3时,6p2+1=6×(5k+3)2+1=150k2+180k+55=5(30k2+36k+11)能被5整除,
∴p=5k+3不合适;
当p=5k+4时,4p2+1=4×(5k+4)2+1=100k2+160k+65=5(20k2+32k+13)能被5整除,
∴p=5k+4不合适.
综上可知:当p=5时,4p2+1和6p2+1都是质数.
点评 本题考查了质数与合数,分p=5k、5k+1、5k+2、5k+3、5k+4(k为正整数)五种情况讨论是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
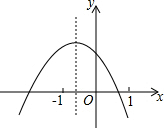 二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)
二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)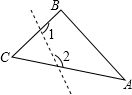 如图,在△ABC中,∠C=40°,若沿图中虚线剪去∠C,则∠1+∠2=120°.
如图,在△ABC中,∠C=40°,若沿图中虚线剪去∠C,则∠1+∠2=120°. 如图,AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=2cm,则AB与CD之间的距离是4cm.
如图,AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=2cm,则AB与CD之间的距离是4cm.