题目内容
1.八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?
分析 (1)根据中位数、众数的定义即可解决.
(2)根据平均数、方差的定义就是即可.
解答 解:(1)甲队成绩的中位数是9.5分,乙队成绩的众数是10分.
故答案分别为9.5,10.
(2)甲队$\overline{x}$=$\frac{7+8+9+7+10+10+9+10+10+10}{10}$=9,s2=$\frac{1}{10}$[(9-7)2+(9-8)2+(9-9)2+(9-7)2+(9-10)2+(9-10)2+(9-9)2+(9-10)2+(9-10)2+(9-10)2]=1.4
乙队$\overline{x}$=$\frac{10+8+7+9+8+10+10+9+10+9}{10}$=9,s2=$\frac{1}{10}$[(9-10)2+(9-8)2+(9-7)2+(9-9)2+(9-8)2+(9-10)2+(9-10)2+(9-9)2+(9-10)2+(9-9)2]=1,
乙队的方差小,所以乙队成绩较为整齐.
点评 本题考查方差、中位数、众数等知识,记住这些知识是解决问题的关键,方差越小成绩越稳定,属于中考常考题型.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
9. 如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
 如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )| A. | 50° | B. | 40° | C. | 80° | D. | 60° |
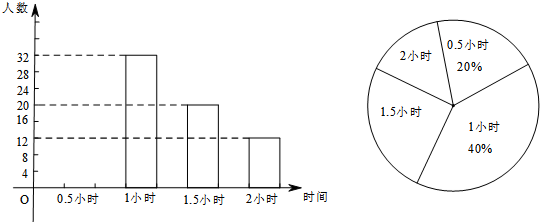
11.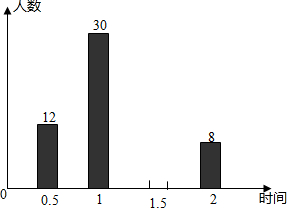 某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
(1)统计表中的m=100,x=50,y=0.08;
(2)被抽样调查的同学劳动时间的众数是1.5,中位数是1.5;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
 某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
某校倡议八年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.5 |
| 2 | 8 | y |
| 合计 | m | 1 |
(2)被抽样调查的同学劳动时间的众数是1.5,中位数是1.5;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
 如图,已知a∥b,如果∠1=52°,那么∠2=52°,∠3=128°,∠4=52°.
如图,已知a∥b,如果∠1=52°,那么∠2=52°,∠3=128°,∠4=52°. 如图,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC,求∠C的度数.
如图,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC,求∠C的度数.