题目内容
3.二次函数y=ax2+bx+c(a≠0)中,若当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值等于( )| A. | -$\frac{b}{2a}$ | B. | $\frac{b}{2a}$ | C. | $\frac{4ac-{b}^{2}}{4a}$ | D. | c |
分析 由抛物线的对称性可知抛物线的对称轴为直线x=-$\frac{b}{2a}$=$\frac{{x}_{1}+{x}_{2}}{2}$,进而可得出x1+x2=-$\frac{b}{a}$,将x=-$\frac{b}{a}$代入二次函数解析式中求出y值,即可得出结论.
解答 解:∵当x取x1,x2(x1≠x2)时,函数值相等,
∴抛物线的对称轴为直线x=-$\frac{b}{2a}$=$\frac{{x}_{1}+{x}_{2}}{2}$,
∴x1+x2=-$\frac{b}{a}$,
∴当x=x1+x2时,y=a×(-$\frac{b}{a}$)2+b×$\frac{b}{a}$+c=c.
故选D.
点评 本题考查了二次函数图象上点的坐标特征以及二次函数的性质,利用抛物线的对称轴找出x1+x2=-$\frac{b}{a}$是解题的关键.

练习册系列答案
相关题目
8. 关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
 关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )| A. | $\frac{4}{3}$ | B. | -1 | C. | -5 | D. | -8 |
5. 如图,已知a∥b,∠2=70°,则下列正确的是( )
如图,已知a∥b,∠2=70°,则下列正确的是( )
 如图,已知a∥b,∠2=70°,则下列正确的是( )
如图,已知a∥b,∠2=70°,则下列正确的是( )| A. | ∠5=70° | B. | ∠8=70° | C. | ∠7=70° | D. | ∠6=110° |
12.在平面直角坐标系中,若点A (a,-b)在第一象限内,则点B (a,b-3)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
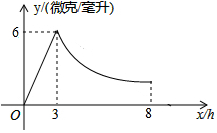 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.
某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.