(1)如图.△ABC中.∠C=90°.那么:①∠A+∠B=90°,②tanA•tanB的值为1,(2)①tan40°•tan50°的值为1,②tan35°•tan45°•tan55°的值为1．题目和参考答案——青夏教育精英家教网—

题目内容

14．

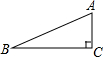（1）如图，△ABC中，∠C=90°，那么：①∠A+∠B=90°；②tanA•tanB的值为1；
（2）①tan40°•tan50°的值为1；②tan35°•tan45°•tan55°的值为1．

分析（1）根据余角的性质，可得答案，根据一个余切等于它余角的余切，可得答案；
（2）根据一个余切等于它余角的余切，可得答案．

解答解：（1）如图，△ABC中，∠C=90°，那么：①∠A+∠B=90°；②tanA•tanB=tanactoA=1的值为 1；
（2）①tan40°•tan50°=tan40°•cto40°=1；
②tan35°•tan45°•tan55°的值为 1，
故答案为：90，1，1，1．

点评本题考查了特殊角的三角函数值，利用同角的关系是解题关键．

练习册系列答案

中考一路领航系列答案

初中毕业生学业水平巩固与提高系列答案

安童教育中考模拟试卷系列答案

考必胜小学毕业升学考试试卷精选系列答案

5．正比例函数y=kx的图象经过直线y=x+1与y=3x+5的交点，那么y=kx的图象位于（　　）

2．二次函数y=5（x-1）（x+3）的图象与y轴交点的坐标是（0，-15）．

9．在△ABC中，∠A：∠B：∠C=4：3：2，且△ABC≌△DEF，则∠E=60°．

19．已知等腰直角三角形斜边上的中线为5cm，则以直角边为边的正方形的面积为（　　）

6．如图1，在平面直角坐标系xOy中，抛物线y=-x²-（m-1）x+m²-6交x轴于点A，D，交y轴正半轴于点B（0，3），顶点C位于第二象限，连接AB，AC，BC．
（1）求抛物线的解析式；
（2）点E是y轴正半轴上一点，且在B点上方，∠ECB=∠CAB，求证：CE是△ABC外接圆的切线；
（3）试探究坐标轴上是否存在一点P，使以B，D，P为顶点的三角形与△ABC相似，若存在，请求出所有点P的坐标；若不存在，请说明理由；
（4）图2中，设与△AOB重合的△EFG从△AOB的位置出发，沿x轴负方向平移t个单位长度（0＜t≤$\frac{3}{2}$）时，△EFG与△ABC重叠部分的面积为S，求S与t之间的函数关系式．

3．已知一点到圆的最小距离为3cm，最大距离为7cm，则圆的半径为（　　）

6．计算“-3的平方除以-2的立方，所得的商减去2，差是多少？”的算式是（-3）²÷（-2）²-2．

试题分类