题目内容
5.在△ABC中,∠A=60°,高BE、CF相交于点O,则∠BOC=120°或60°.分析 分为两种情况,画出图形后根据内角和定理求出即可.
解答 解:分为两种情况:
①如图1,∵高BE、CF交于点O,
∴∠AFO=∠AEO=90°,
∵∠A=60°,
∴∠BOC=∠EOF=360°-90°-90°-60°=120°;
②如图2,∵高BE、CF交于点O,
∴∠BFO=∠AEB=90°,
∵∠A=60°,∠ABE=∠OBF,
∴∠BOC=∠A=60°;
综上所述,∠BCO=120°或60°.
故答案为:120°或60°.
点评 本题考查了对三角形内角和定理和垂直定义的应用,解题时注意:三角形的内角和等于180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.使代数式$\frac{1}{\sqrt{x+3}}$+$\sqrt{4-3x}$有意义的整数x有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
16.已知a<b,下列四个不等式中正确的是( )
| A. | 3a>3b | B. | -a<-b | C. | a+3<b+3 | D. | a-6>b-6 |
13.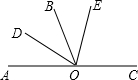 如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )
如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )
 如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )
如图:若∠AOB与∠BOC是一对邻补角,OD平分∠AOB,OE在∠BOC内部,并且∠BOE=$\frac{1}{2}$∠COE,∠DOE=72°.则∠COE的度数是( )| A. | 36° | B. | 72° | C. | 44° | D. | 56° |
20.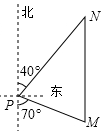 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )| A. | 40海里 | B. | 60海里 | C. | 70海里 | D. | 80海里 |
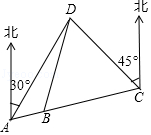 如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.
如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.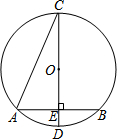 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为4cm.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为4cm.