题目内容
17.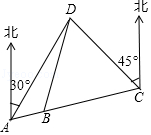 如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.
如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.(1)求∠ADC的度数;
(2)求A、D两地的距离.
分析 (1)求出∠DCA的度数,再判断出BC=CD,据此即可判断出△BCD是等边三角形.
(2)过点B作BE垂直于AD,垂足为E,求出∠DAC的度数,判断出△BCD是等边三角形,再利用三角函数求出AB的长,从而得到AB+BC+CD的长.
解答 解:(1)由题意可知∠DCA=180°-75°-45°=60°,
∵BC=CD,
∴△BCD是等边三角形
∴∠BDC=∠DBC=60°,
∵∠DAB=75°-30°=45°,
∵∠DBC=∠ADB+∠DAB,
∴∠ADB=15°,
∴∠ADC=∠ADB+∠BDC=15°+60°=75°.
(2)解:过点B作BE垂直于AD,垂足为E,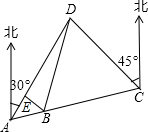
由题意可知∠DAC=75°-30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60° BD=BC=CD=30m,
∴∠ADB=∠DBC-∠DAC=15°,
∴BE=BD•sin15°≈0.26×30≈7.8m,DE=BD•cos15°≈0.97×30≈29.1m,
∵∠EAB=∠EBA=45°,
∴AE=EB=7.8m,
∴AD=AE+DE=7.8+29.1≈37m.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 如图,两个等直径圆柱构成如图所示的T型管道,则其俯视图正确的是( )
如图,两个等直径圆柱构成如图所示的T型管道,则其俯视图正确的是( )



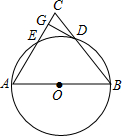 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.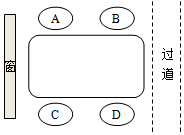 莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,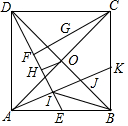 如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )
如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )