题目内容
9. 如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.
如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.
分析 根据正方形的面积为边长的平方可知AB2和BC2的值,再根据勾股定理即可求出R所代表的正方形的边长.
解答 解:∵AB2=89,BC2=25,∠C=90°,
∴AC2=89-25=64,
∴字母B所代表的正方形的边长=$\sqrt{64}$=8.
故答案为:8.
点评 本题考查了直角三角形中勾股定理的运用,本题中根据勾股定理求斜边长的平方是解本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
19.如果把代数式$\frac{x+y}{xy}$中的x与y都扩大到原来的8倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的8倍 | ||
| C. | 缩小为原来的$\frac{1}{8}$ | D. | 扩大为原来的16倍 |
17.数据10,15,15,20,40的众数是( )
| A. | 15 | B. | 17.5 | C. | 20 | D. | 40 |
4.已知直线a:y=kx(k≠0)和直线b:y=kx+1(k≠0),则说法正确的是( )
| A. | 直线a向上平移1个单位得到直线b | B. | 直线a向下平移1个单位得到直线b | ||
| C. | 直线a向左平移1个单位得到直线b | D. | 直线a向右平移1个单位得到直线b |
6.$\sqrt{4-x}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥4 | B. | x>4 | C. | x≤4 | D. | x<4 |
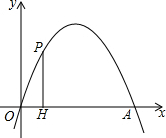 如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.
如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.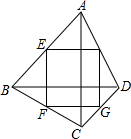 几何证明.
几何证明.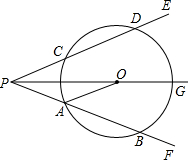 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE