题目内容
19.如果把代数式$\frac{x+y}{xy}$中的x与y都扩大到原来的8倍,那么这个代数式的值( )| A. | 不变 | B. | 扩大为原来的8倍 | ||
| C. | 缩小为原来的$\frac{1}{8}$ | D. | 扩大为原来的16倍 |
分析 根据x与y都扩大到原来的8倍,分别判断出x+y、xy的变化情况,即可判断出这个代数式的值的变化情况.
解答 解:∵x与y都扩大到原来的8倍,
∴x+y扩大到原来的8倍,xy扩大到原来的64倍,
∴这个代数式的值缩小为原来的$\frac{1}{8}$.
故选:C.
点评 此题主要考查了分式的基本性质的应用,要熟练掌握,解答此题的关键是分别判断出x+y、xy的变化情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.平面直角坐标系内点P(m,2),与Q(-1,n)关于原点对称,则下列结果正确的是( )
| A. | m=1,n=-2 | B. | m=-1,n=2 | C. | m=-1,n=-2 | D. | m=1,n=2 |
14.如果一组数据:6,-2,0,6,4,x的平均数是2,那么x等于( )
| A. | 3 | B. | 4 | C. | -2 | D. | 6 |
11.不等式-2x-1≥1的解集是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≤0 | D. | x≤1 |
8.在某次体育活动中,统计九年级1,2班学生每分钟跳绳的成绩(单位:次)情况如表:下面3种说法错误的是( )
①1班学生的平均成绩高于2班学生的平均成绩
②1班学生成绩的波动比2班学生成绩的波动小
③1班学生成绩优秀的人数(跳绳次数≥150)不会多于2班学生成绩优秀的人数.
| 参加人数 | 平均次数 | 中位数 | 方差 | |
| 1班 | 50 | 135 | 151 | 110 |
| 2班 | 50 | 135 | 149 | 190 |
②1班学生成绩的波动比2班学生成绩的波动小
③1班学生成绩优秀的人数(跳绳次数≥150)不会多于2班学生成绩优秀的人数.
| A. | ① | B. | ② | C. | ③ | D. | ①和③ |
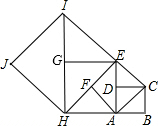 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014. 如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.
如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.