题目内容
1.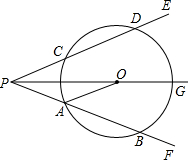 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE(1)求证:AP=AO;
(2)若弦AB=12,求tan∠OPB的值.
分析 (1)由PG平分∠EPF可得∠CPO=∠APO,由AO∥PD可得∠CPO=∠AOP,从而有∠APO=∠AOP,则有AP=AO.
(2)过点O作OH⊥AB于H,如图2.根据垂径定理可得AH=BH=6,从而可求出PH,在Rt△AHO中,运用勾股定理可求出OH,然后运用锐角三角函数的定义就可解决问题.
解答 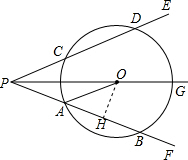 (1)证明:如图,
(1)证明:如图,
∵PG平分∠EPF,
∴∠CPO=∠APO.
∵AO∥PD,
∴∠CPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO.
(2)解:过点O作OH⊥AB于H,如图.
根据垂径定理可得AH=BH=$\frac{1}{2}$AB=6,
∴PH=PA+AH=AO+AH=10+6=16.
在Rt△AHO中,
OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=$\sqrt{100-36}$=8,
∴tan∠OPB=$\frac{OH}{PH}$=$\frac{8}{16}$=$\frac{1}{2}$.
∴tan∠OPB的值为$\frac{1}{2}$.
点评 本题考查了垂径定理、等腰三角形的判定与性质、勾股定理、锐角三角函数的定义、平行线的性质、角平分线的定义等知识,综合性比较强.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
11.不等式-2x-1≥1的解集是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≤0 | D. | x≤1 |
16.甲、乙两家电器商场以相同价格试销同一种品牌电视机.在10天中,两家商场的日销售量分别统计如表:(单位:台)
(1)求甲、乙两家商场的日平均销量;
(2)甲、乙两家商场每天销售的中位数分别是多少?
(3)在10天中,哪家商场的销售量更稳定?为什么?
| 甲商场销量 | 1 | 3 | 2 | 3 | 0 | 1 | 2 | 3 | 1 | 4 |
| 乙商场销量 | 4 | 0 | 3 | 0 | 3 | 3 | 2 | 2 | 0 | 3 |
(2)甲、乙两家商场每天销售的中位数分别是多少?
(3)在10天中,哪家商场的销售量更稳定?为什么?
 如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.
如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.