题目内容
14. 几何证明.
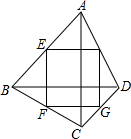
几何证明.如图,已知四边形ABCD的两条对角线AC和BD互相垂直且相等,顺次连接该四边形四边的中点E、F、G、H.试判断四边形EFGH的形状并证明.
分析 四边形EFGH的形状是正方形,先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
解答 解:四边形EFGH的形状是正方形,
理由如下:
在△ABC中,F、G分别是AB、BC的中点,
故可得:FG=$\frac{1}{2}$AC,同理EH=$\frac{1}{2}$AC,GH=$\frac{1}{2}$BD,EF=$\frac{1}{2}$BD,
在四边形ABCD中,AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AD、CD的中点,
则EH∥AC,
同理GH∥BD,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.
点评 此题考查了正方形的判定,解题的关键是了解既是矩形又是菱形的四边形是正方形,难度适中.

练习册系列答案
相关题目
2.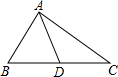 如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )
如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )
 如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )
如图,在Rt△ABC中,∠BAC=90°,AB=6,D是斜边BC的中点,若AD=5,则AC等于( )| A. | 8 | B. | 64 | C. | 5$\sqrt{2}$ | D. | 6$\sqrt{3}$ |
19.式子$\frac{\sqrt{2{x}^{2}+1}}{x-1}$有意义的x的取值范围是( )
| A. | x≥0且x≠1 | B. | x≠1 | C. | x≥-$\frac{1}{2}$ | D. | x≤0且x≠-1 |
11.已知点A(1,y1)、B(2,y2)在反比例函数y=$\frac{6}{x}$ 的图象上,则y1、y2大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
 如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.
如图,分别以Rt△ABC的三边为边长,在三角形外作三个正方形,若正方形P的面积等于89,Q的面积等于25,则正方形R的边长是8.