题目内容
在△ABC中,AB=3,BC=
,∠A=30°,则△ABC的面积为 .
| 3 |
考点:解直角三角形
专题:
分析:此题所给条件是:已知三角形的两边及一边的对角此三角形不唯一,所以应分两种情况:①当∠B为锐角时,②当∠B为钝角时,然后过点B作AC的高,由勾股定理可得出三角形的底和高,再求面积即可.
解答:解:当∠B为钝角时,如图1,
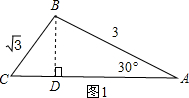
过点B作BD⊥AC,
∵∠BAC=30°,
∴BD=
AB,
∵AB=3,
∴BD=
,
由勾股定理可得:
AD=
=
,
∵BC=
,
∴由勾股定理得:CD=
=
,
∴AC=CD+AD=2
,
∴S△ABC=
AC•BD=
×2
×
=
;
当∠C为钝角时,如图2,
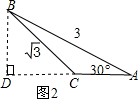
过点B作BD⊥AC,交AC延长线于点D,
∵∠BAC=30°,
∴BD=
AB,
∵AB=3,
∴BD=
,
∵BC=
,
∴由勾股定理得:CD=
=
,AD=
=
,
∴AC=AD-DC=
,
∴S△ABC=
AC•BD=
×
×
=
.
故答案为:
或
.

过点B作BD⊥AC,
∵∠BAC=30°,
∴BD=
| 1 |
| 2 |
∵AB=3,
∴BD=
| 3 |
| 2 |
由勾股定理可得:
AD=
| AB2-BD2 |
3
| ||
| 2 |
∵BC=
| 3 |
∴由勾股定理得:CD=
| BC2-BD2 |
| ||
| 2 |
∴AC=CD+AD=2
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
当∠C为钝角时,如图2,

过点B作BD⊥AC,交AC延长线于点D,
∵∠BAC=30°,
∴BD=
| 1 |
| 2 |
∵AB=3,
∴BD=
| 3 |
| 2 |
∵BC=
| 3 |
∴由勾股定理得:CD=
| BC2-BD2 |
| ||
| 2 |
| AB2-BD2 |
3
| ||
| 2 |
∴AC=AD-DC=
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
3
| ||
| 4 |
故答案为:
3
| ||
| 2 |
3
| ||
| 4 |
点评:本题考查了解直角三角形,还涉及到的知识点有勾股定理、直角三角形的性质,30度的锐角所对的直角边等于斜边的一半.

练习册系列答案
相关题目
线段AB被分为2:3:4三部分,已知第一部分和第三部分的中点间的距离是6.6cm,则线段AB的长为( )
| A、8.9cm |
| B、9.9cm |
| C、10.8cm |
| D、11.7cm |
 如图△ABC与△DEF是位似图形,位似比是1:2,已知DE=4,则AB的长是( )
如图△ABC与△DEF是位似图形,位似比是1:2,已知DE=4,则AB的长是( )| A、2 | B、4 | C、8 | D、1 |
 如图,D、E分别是半径OA和OB的中点,
如图,D、E分别是半径OA和OB的中点,
 如图,点P是△ABC中两外角∠DBC与∠ECB平分线的交点,试探索∠BPC和∠A的数量关系.
如图,点P是△ABC中两外角∠DBC与∠ECB平分线的交点,试探索∠BPC和∠A的数量关系. 如图,已知AE=CF,∠AFD=∠CEB,AD∥BC,求证:△ADF≌△CBE.
如图,已知AE=CF,∠AFD=∠CEB,AD∥BC,求证:△ADF≌△CBE.